Weiss jemand wie diese Aufgabe zu lösen ist?
Eine Torte wird mit zwei zueinander rechtwinkligen Schnitten in vier Stücke aufgeteilt. Dabei wird aber der Mittelpunkt verfehlt, weshalb die Stücke nicht gleich gross sind. Nachdem ein Stück gegessen ist, misst jemand bei den restlichen drei die Länge des gebogenen Randes. Die drei Bögen messen 22, 26 und 28cm. Wie gross kann das gegessene Tortenstück gewesen sein?
2 Antworten
Hallo,
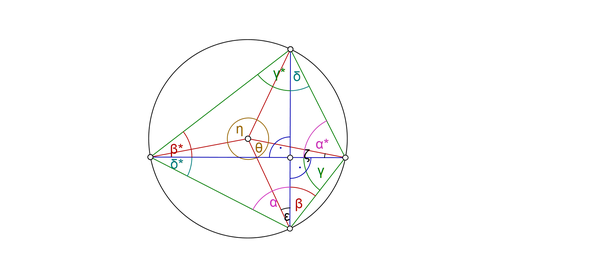
betrachte beigefügte Zeichnung:
Die blauen Linien sind die beiden zueinander senkrechten Schnitte durch die Torte (Kreis). Verbindest Du die Schnittpunkte mit dem Kreis untereinander, bekommst Du ein Sehnenviereck, in dem sich gegenüberliegende Winkel zu 180° ergänzen.
Verbindest Du den Mittelpunkt des Kreises mit diesen Schnittpunkten, entstehen - so behaupte ich - Zentriwinkel, die sich ebenfalls zu 180° ergänzen, wenn sie sich gegenüberliegen.
Behauptung: η+θ=180°
Beweis: (Das Zeichen für Grad ° lasse ich im Beweis weg):
β+γ=90
β+ε=γ+ζ
ε=γ+ζ-β
η+θ=180-2(β-ζ)+180-2(β+ε)
Die roten Linien sind als Kreisradien alle gleich lang, deshalb hast Du es mit gleichschenkligen Dreiecken zu tun, deren Basiswinkel gleich sind.)
η+θ=360-2β+2ζ-2β-2ε=
360-4β+2ζ-2(γ+ζ-β)=
360-4β+2ζ-2γ-2ζ+2β=
360-2β-2γ=
360-2(β+γ)=360-2*90=180
Damit ist bewiesen, daß sich gegenüberliegende Zentriwinkel zu 180° ergänzen, wenn Du ein Sehnenviereck hast, das sich aus der Verbindung der Schnittpunkte eines Kreises mit zwei aufeinander senkrecht stehenden Sehnen ergibt.
Wenn sich die Zentriwinkel aber zu 180° ergänzen, ergänzen sich gegenüberliegende Umkreisabschnitte jeweils zu einem Halbkreis.
So könnte das fehlende Tortenstück - lag es beispielsweise dem Stück mit 26 cm Rand gegenüber, diese 26 cm zu 22+28=50 cm ergänzen, also einen Rand von 24 cm besessen haben.
Auch andere Größen sind möglich, je nachdem, welche Stücke sich gegenüber lagen.
Herzliche Grüße,
Willy
Es gibt vier mögliche Lösungen:
x/22 = 26/28
x/22 = 28/26
x/28 = 22/26
x/28 = 26/22