Stellen Sie fest, für welche t Element der Reellen Zahlen die folgenden Bedingungen gelten?
Was soll ich hier machen? :D
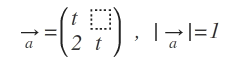
2 Antworten
Nutzer, der sehr aktiv auf gutefrage ist
|a|=Wurzel(a_1²+a_2²) , wobei a_1 der erste Eintrag des Vektors ist. Du musst also deinen Vektor in die Formel einsetzen und schauen, wann 1 rauskommt.
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik
Ich denke, die Betragsstriche sollen die Determinante der Matrix a bedeuten.
Woher ich das weiß:Studium / Ausbildung – Masterabschluss Theoretische Physik