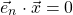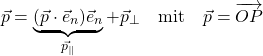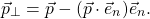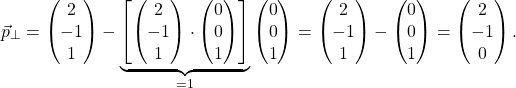Orthogonalprojektion mit Normalenvektor?
Hallo,
für eine Ebene der Form:
E: ax+by+cz=0
wie leitet man hier die Orthogonalprojektion eines Punktes auf diese Ebene her?
2 Antworten
Also du kannst hier direkt den Normalenvektor der Ebene ablesen.
Nämlich n=(a,b,c)
Sei jetzt x=(x1,x2,x3) ein Punkt im R^3, den du du auf die Ebene abbilden willst.
Zuerst bildest du eine Lotgerade L, die senkrecht zu E ist und durch x geht.
Also:
L: x+s*n
Was gleich den Koordinaten
(x1+s*a,x2+s*b,x3+s*c) ist
Diesen Punkt setzt du nun in die Ebene ein:
a*(x1+s*a)+b*(x2+s*b)+c*(x3+s*c)=0
Dies musst du nur noch nach s umstellen, was du dann als Parameter in die gerade Gleichung L einsetzt. Dann dann hast du die allgemeine Form für die Projektion
Ein Vektor x liegt genau dann in der Ebene durch den Ursprung O, wenn er die Gleichung
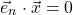
erfüllt, wobei ich mit e_n den Normalenvektor der Ebene bezeichne. Nun kannst du aber den Ortsvektor eines Punktes P zerlegen in einen zur Normalenrichtung parallelen und einen orthogonalen Anteil. Am orthogonalen Anteil bist du interessiert, denn genau dies ist die gesuchte Projektion. Es gilt also
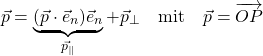
bzw.
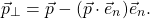
Wir können ein Beispiel betrachten. Nehmen wir an, wir würden gerne die Projektion des Punktes (2, -1, 1) auf die x-y-Ebene wissen. Das ist natürlich sehr schnell im Kopf bestimmt, denn die Projektion erhalten wir, indem wir lediglich die dritte Koordinate vernachlässigen bzw. zu 0 machen. Wir können das aber auch rechnerisch nachprüfen. Gemäß unserer Formel gilt nämlich
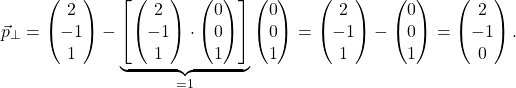
Wir erhalten also genau das erwartete Ergebnis.