Matheproblem bitte helfen! (Anwendung quadratischer Funktionen)
Hier die Aufgabenstellung, benötige dringend Hilfe, weil ich demnächst eine Klausur schreibe und das nicht verstehe:
a)Die Flugbahn eines Golfballes kann näherungsweise durch eine Parabel beschrieben werden, wobei x der horizontalen Entfernung vom Abschlagspunkt in Metern und f (x) der Höhe des Balles in Metern entspricht. Eine spezielle Flugbahn kann durch die Gleichung f (x) = -0,006x² + 0,9 x beschrieben werden.
(1) Wie weit ist der Ball über der 100-m-Markierung (100 m horizontale Entfernung vom Abschlagspunkt) von der Erde entfernt?
(2) Wie weit fliegt der Ball?
(3) Wie hoch ist der Ball in seinem höchsten Punkt?
Bitte extra ausführlich für Vollpfeifen schreiben, danke im Voraus!
3 Antworten
Zu (2) etwas ausführlicher:
Gesucht sind ist der Abstand zwischen den Nullstellen "Aussgangspunkt" und "Auftreffpunkt" der Parabel, weil genau dort die Höhe f(x) jeweils 0 ist.
0 = -0,006x² + 0,9 x = (-0,006x+ 0,9)x , also
x1 = 0 oder aber
-0,006x+ 0,9 = 0
-0,006x = - 0,9
x2 = - 0,9 / (-0,006) = 900 / 6 = 300 / 2 = **150 (m)
(3) geht sehr viel einfacher:
Eine Parabel ist immer achsensymmetrisch zu einer y-Parallelen durch ihren Scheitel. Also ist der x-Wert d des Scheitels immer der Mittelwert der Nullstellen; hier:
d = ( 0 + 150 ) / 2 = 75 (m)
Einsetzen ergibt
f(75) = 33,75 (m)
(siehe markkraft)
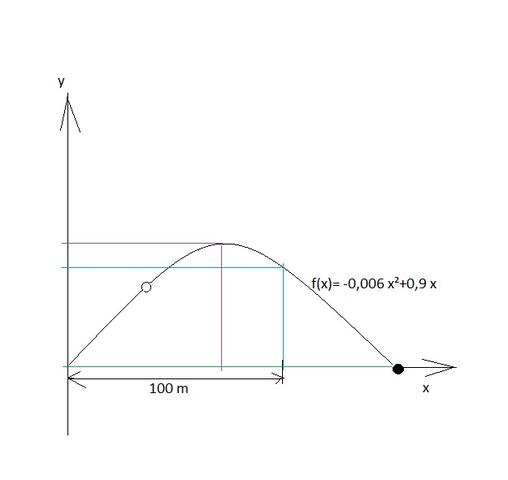
Ich hab dir mal eine Skizze dazu gemacht. Vielleicht siehst du es dann leichter was gesucht wird.
1) Das ist in der Zeichnung die blaue Markierung. Du kennst also den x-Wert nämlich 100 m und sollst den y-Wert dazu berechnen, bzw. f(100). Dazu setzt du x einfach ein
f(100)= -0,006 * 10.000+0,9 * 100
= -60+90=30
Er ist also 30 m über der Erde
2) Wie weit fliegt der Ball hat psychironiker ja schon erklärt und du siehst es auch in der Zeichnung. Es ist der Abstand vom 1. Nullpunkt (Abschlag) zum 2. Nullpunkt (Aufschlag), also musst du die Funktion gleich Null setzen
-0,006 x²+0,9 x=0
Das geht hier sehr gut ohne pq-Formel, da es nur Summanden mit x gibt. Deshalb einfach x ausklammern und anwenden, dass ein Produkt immer dann Null ist wenn mindestens ein Faktor gleich Null ist.
x * ( -0,006 x+0,9)=0
x=0 und/oder
-0,006x+0,9=0 => x=0,9 / 0,006=150
Also fliegt er 150 m weit.
3) Das ist die violette Markierung, also der Scheitelpunkt deiner Funktion. Die Methode von psychironiker ist die leichteste, aber ich fürchte, dein Lehrer will die Scheitelpunktform sehen. Das geht mit der quadratischen Ergänzung, die schon markkraft vor gerechnet hat. ich mach es jetzt nur noch mal für "Vollpfeifen" ;-))
f(x)= -0,006 x²+0,9 x -> -0,006 ausklammern
f(x)= -0,006(x²-150 x) -> 150=2b, also b=75 und b²=5625. b² wird addiert, damit man die binomische Formel anwenden kann, aber gleich wieder subtrahiert, damit man den Wert nicht verändert.
f(x)= -0,006(x²-150 +5625-5625) -> bei den ersten drei Summanden in der Klammer wende ich die bin. Formel an, der 4. bleibt einfach stehen
f(x)= -0,006[(x-75)²-5625] -> jetzt muss ich noch die eckige Klammer auflösen
f(x)= -0,006(x-75)²+33,75
f(x)=......a.....(x-xs)².+..ys
Jetzt kannst du ablesen: xs=75 und ys=33,75
S(75|33,75)
- f(100) = 30m
- f(x) = 0 => x1 = 0 oder x2 = 150, daher fliegt der Ball 150m weit
- f(x) = -3/500·x² + 9/10·x | : (-3/500)
-500/3·f(x) = x² - 150x | quadratische Ergänzung: + (p/2)²
-500/3·f(x) = x² - 150x + 5625 - 5625 | Mit binomischer Formel faktorisieren
-500/3·f(x) = (x - 75)² - 5625 | · (-3/500)
f(x) = -3/500·(x - 75)² + 135/4
Daher, ist der Scheitelpunkt bei (75; 33,75). Der Ball ist an seinem höchsten Punkt 33,75m über der Erde.
LG Mark