Kann mir jemand helfen bitte Pyramiden Seitenhöhe zu berechnen?

2 Antworten
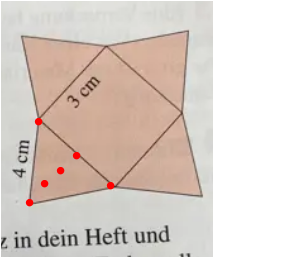
Seitenhöhe eingezeichnet.
Sie teilt das Dreieck in zwei gleiche Dreiecke mit einem rechten Winkel.
Eins davon nimmt man
Es hat drei Seiten : Höhe , 3/2 und 4
Pythagoras : Hypotenuse gegenüber dem rechten Winkel ist
4² = (3/2)² + H²
4² - (3/2)² = H²
16 - 2.25 = H²
wurzel(13.75) = H
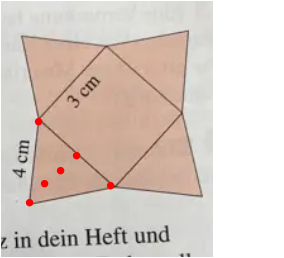
Trage eine Seitenhöhe ein. Diese steht rechtwinklig auf der Grundseite des Dreiecks und teilt dieses in zwei rechtwinklige Dreiecke. Die Seitenhöhe ist eine Kathete und die halbe Grundseite ist die zweite Kathete eines dieser rechtwinkligen Dreiecke. Die Hypotenuse ist mit 4 cm gegeben. Nutze den Satz des Pythagoras, um die Seitenhöhe zu bestimmen.
Die vier Seiten der Pyramide sind Dreiecke mit der Grundseite von 3 cm (Grundkante Pyramide) und den beiden Seitenlängen (Seitenkanten der Pyramide) von jeweils 4 cm.
Die Höhe auf die Grundseite eines dieser Dreiecke teilt diese mittig. Es entstehen zwei rechtwinklige Dreiecke mit den Katheten 1,5 cm und h_a sowie der Hypotenuse von 4 cm.
Trage eine Seitenhöhe in die Skizze ein!
Es gilt nach Pythagoras:
h_a² = 4² - 1,5²
Wäre nett wenn du das zeigen könntest