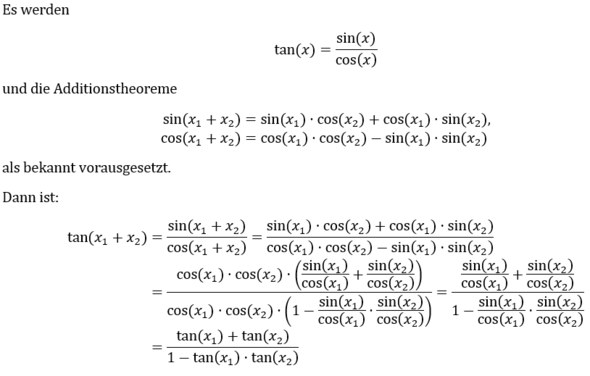Die Aufgabe lautet: Zeigen Sie Tan ( x1+x2) =tanx1+tanx2/1-tanx1*tanx2?

Benutze:

e^(ix) = cos(x) + i*sin(x)

Damit folgt:

e^(i(x1 + x2)) = e^(ix1) * e^(ix2) = (cos(x1) + i*sin(x1)) * (cos(x2) + i*sin(x2))

Damit folgern wir die folgenden Additionstheoreme:

cos(x1 + x2) = cos(x1)cos(x2) - sin(x1)sin(x2)

sin(x1 + x2) = cos(x1)sin(x2) + cos(x2)sin(x1)

Damit folgt:

tan(x1 + x2) =

= (cos(x1)sin(x2) + cos(x2)sin(x1))/(cos(x1)cos(x2) - sin(x1)sin(x2))

Ausklammern von cos(x1)cos(x2) im Zähler liefert:

= (sin(x2)/cos(x2) + sin(x1)/cos(x1))*cos(x1)cos(x2)/(cos(x1)cos(x2) - sin(x1)sin(x2))

Nun Klammern wir aus dem Nenner cos(x1)cos(x2) aus:

= (sin(x2)/cos(x2) + sin(x1)/cos(x1))*cos(x1)cos(x2)/[ {cos(x1)cos(x2)}*(1  - sin(x1)sin(x2)/(cos(x1)cos(x2))) ]

Da nun im Zähler und Nenner der Faktor cos(x1)cos(x2) steht folgt durch kürzen unter der Bedingung:  |cos(x1)cos(x2)| > 0

= (sin(x2)/cos(x2) + sin(x1)/cos(x1))/(1  - sin(x1)sin(x2)/(cos(x1)cos(x2)))

Benutzen der Definitionsgleichung für den Tangens: tan(x) = sin(x)/cos(x) ; liefert uns damit final:

= (tan(x2) + tan(x2))/(1 - tan(x1)*tan(x2))

Wir erhalten somit die gesuchte Identität:

tan(x1 + x2) = (tan(x2) + tan(x2))/(1 - tan(x1)*tan(x2))

unter der Bedingung:   |cos(x1)cos(x2)| > 0

Eine Option wäre:

tan(a + b) = sin(a + b) / cos(a + b)

Ab hier die Additionstheoreme anwenden.

Dann wieder in den tan zurückführen.

Viel Spaß ;)

Eine Möglichkeit ist es, die Additionstheoreme für sin und cos auszunutzen, falls diese als bekannt vorausgesetzt werden.

Siehe: Bild im Anhang