Berechnung einer Fläche, in der 2 Kreise sich überschneiden
hi, ich habe in Mathe ein Problem. Es gibt einen großen Kreis,in dem sind 2 kleine ,sich überschneidene Kreise. Nun sollen wir die Fläche , die nicht die 2kleinen Kreise sind,im großen Kreis,berechnen. Wir wissen aber nur,dass der Radius vom großen Kreis 10cm ist,und die Mittelpunkte der 2kleinen Kreise 5cm auseinander liegen.Kann mir das vlllt jemand helfen? danke schonmal!
5 Antworten
Solange man nicht die Radien der kleinen Kreise kennt, kann man nichts berechnen.
R1 = 10cm Die Mittelpunkte liegen 5cm auseinander, also um möglichst große Kreise zu zeichnen, kann ein Innenkreis den Aussenkreis berühren: R1 - 2,5 cm = 7,5 cm
Die Innenkreise können einen Radius bis 7,5 cm besitzen!
vielen Dank,aber den Flächeninhalt abzüglich der kleinen Kreise kann man mit den Angaben jetzt nicht bestimmen,oder?
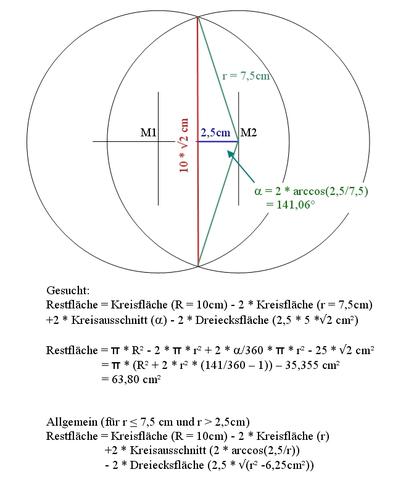
Im Bild ist der Sonderfall gerechnet, dass die kleinen Kreise gleichgroß sind und den Außenkreis berühren.
Auserdem findest Du den Ansatz, wenn die kleinen Kreise gleichgroß sind, aber nicht den Außenkreis berühren
Lösung !
Großer Kreis --->A =3,14 * 10 cm² * 2 = 628 cm² / Ergebnis>> Restfläche rund 288 cm²!!
Kleiner Kreis ---> A = 3,14 * 5 * 2 = 157 cm
Kleiner Kreis Fläche 2 mal = 314 cm²
Nun den Kreisbogen des eine kleinen Kreises abziehen !
A bogen =3,14 * 25cm² * 120° / 360 ° =26,16 cm²--->628 - 314 -26,16 = 288 cm² !
Ich habe einen Link gefunden, vielleicht hilft dieser dir weiter:
http://www.mathe1.de/mathematikbuch/geometrie_kreisflache_125.htm
Das funktioniert aber nur, wenn sich die Kreise genau im Mittelpunkt schneiden!