Ableitungsgraph?
Kann mir bitte jemand bei dieser Aufgabe helfen?
Der Ausgangsgraph und abgeleitete Graph sollten in einer Tabelle angeordnet sein.
Ich bin mir leider nicht sicher, wie es geht , weil ich lange krank war. Vielen Dank für eure Mühe 🤗
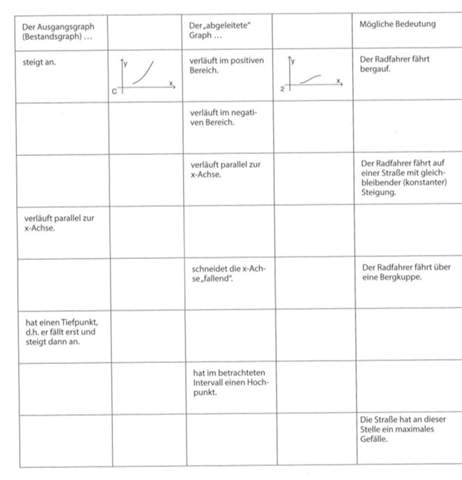
.
4 Antworten
Straße hat an der Stelle ein maximales Gefälle → f´(x)=m<0 hat ein Minimum und ist negativ (liegt unter der x-Achse) → 6
Der dazugehörige Grapg y=f(x)=.. muß dann monoton fallend sein und eine Stelle haben,wo es am steilsten nach unten geht → Minimum von f´(x)=m
Graph y=f(x)=.. G ist monoton fallend f´(x)=m<0 und hat eine Stelle,wo er am steilsten fällt.
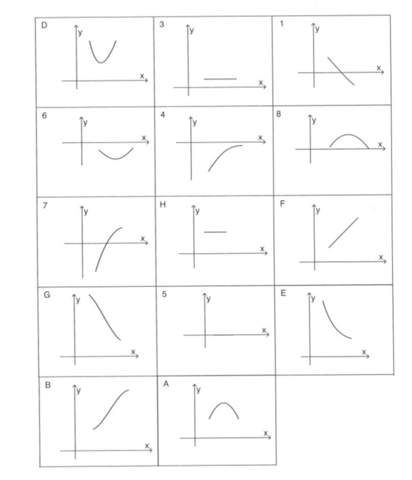
Die Ausgangsfunktionen sind mit großen Buchstaben gegenzeichnet (siehe unten → Bilder)
die Ableitungsfunktionen f´(x)=m=.. sind mit Nummern gekennzeichnet (siehe unten → Bilder
f´(x)=m=konstant → verläuft parallel zur x-Achse Bild 3 und F
F ist eine Gerade der Form y=f(x)=m*x+b Steigung f´(x)=m=konstant
Graph y=f(x)=konstant → H verläuft parallel zur x-Achse → Steigung f´(x)=m=0 5
Radfahrer fährt auf eine ebene Straße (keine Steigung)
den Rest schaffst du wohl selber
Hast das denn nun mit den ableiten begriffen ?
1) der Graph ist monoton fallend ,dann Ableitungsfunktion y´=f´(x)=m<0 → liegt unter der x-Achse.
2) der Graph ist monoton steigend,dann Ableitungsfunktion y´=f´(x)=m>0 → liegt über der x-Achse
3) hat der Graph Extrema,Maximum/Minimum,dann hat dort die Ableitungsfunktion y´=f´(x)=m eine Nullstelle mit der x-Achse
Übungsbeispiele:
zeichne folgende Graphen
1) y1=f1(x)=0,5*x abgeleitet y´=f´(x)=m=0,5=konstant
2) y2=f2(x)=-1*x abgeleitet y´=f´(x)=m=-1=konstant
3) y3=f3(x)=1*x² abgeleitet y´=f´(x)=2*x ist eine Gerade der Form y=f(x)=m*x
Graph hat einen Tiefpunkt d.h. fällt und steigt dann wieder
y=f(x)=.. → G Ableitungsfunktion f´(x)=m=.. 7
Steigung vor dem Tiefpunkt f´(x)=m<0 negativ
Steigung nach dem Tiefpunkt f´(x)=m>0 positiv
im Tiefpunkt f´(x)=m=0 Nullstelle der Ableitungsfunktion
Bedingung Minimum (Tiefpunkt) f´(x)=0 und f´´(x)>0
Bedeutung → Fahrradfahrer fährt durch eine Senke
f´(x)=m=.. schneidet die x-Achse danach ist die Steigung fallend. 1
y=f(x)=.. A einen aufsteigender Ast → f´(x)=m>0 positiv
dann ein abfallender Ast → f´(x)=m<0 negativ
Deutung Fahrradfahrer fährt einen Berg hoch → über einen Hügel und fährt dann wieder bergab
Vielen Dank dafür ❤️