Bestimme die Punkte mit dem Abstand 3 von der Ebenen?
Hallo zusammen,
Kann mir jemand vielleicht sagen wie ich da vorgehen soll bei dieser Aufgabe . Dachte ich setzte die Gerade(als Punkte) in die HNF ein und setzt das dann gleich drei. Aber irgendwie stimmt mein Ergebnis nicht mit der Lösung überein. Wäre dankbar für eure Hilfe😊🙂

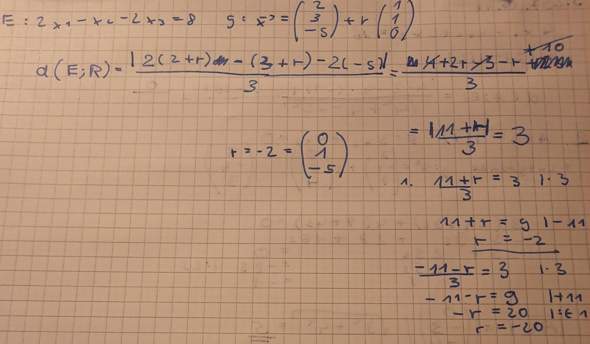
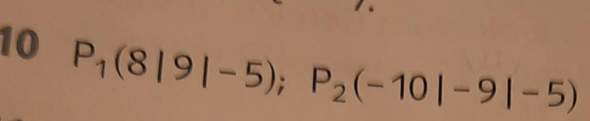
Das ist die Lösung die haben für r 1 und 2 raus kann mir bitte jemand sagen was ich falsch gemacht habe danke😊
1 Antwort

2 + r
g(r) = 3 + r
-5
Der Normalenvektor der Ebene lautet n = (2,-1,-2). Dieser steht senkrecht auf der Ebene. Man wählt man einen beliebigen Punkt auf der Geraden g als Ortsvektor und n als Richtungsvektor. Das ergibt eine Schar von Geraden, die alle auf der Ebene senkrecht stehen:
2 + r + s*2
h(r,s) = 3 + r - s
-5 - s*2
Diese Geraden in die Ebene einsetzen, die Lösung ergibt die entsprechenden Schar von Lotfußpunkten:
2*(2+r+2*s) - (3+r-s) - 2*(-5-2s) = 8
Das aufgelöst ergibt s = -r/9 - 1/3
s in h einsetzen:
2 + r + (-r/9 - 1/3)*2 4/3 + 7/9*r
h(r) = 3 + r - (-r/9 - 1/3) = 10/3 + 10/9*r
-5 - (-r/9 - 1/3)*2 -13/3 + 2/9*r
Jetzt brauchen wir noch die Abstände von h und g:
[(2 + r) - (4/3 + 7/9*r)]² + [(3 + r) - (10/3 + 10/9*r)]² + [-5 - (-13/3 + 2/9*r)]² = 3²
Das ergibt die quadratische Gleichung
1/9 r² + 2/3 r - 8 = 0
Lösung r1= 6, r2 =-12
Eingesetzt in g(r) ergibt das die gesuchten Punkte.