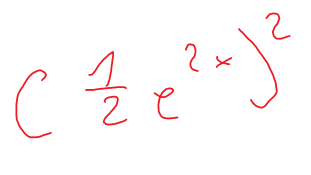Durch die Punkte P=(-3;1)und Q=(-5;-3) gehen unendlich viele Parabeln. Stellen Sie ein lineares Gleichungssystem für die Koeffizienten a, b und c der Parabelgleichung y=ax2+bx+c auf und bestimmen Sie dessen Lösungsmenge. Setzen Sie dabei bitte die von Ihnen gewählte frei wählbare Variable gleich t, damit Ihre Lösung vom System richtig korrigiert werden kann. Verwenden Sie bitte außerdem Brüche und keine gerundeten Werte.
DAS HABE ICH BIS JETZT:
P(-3,1) einsetzen in der Parabel Gleichung:
1=a*(-3)^2+b*(-3)+c=> 9*a-3*b+c=1
Q(-5,-3) einsetzen in der Parabel Gleichung
-3= a*(-5)^2+b*(-5)+c=> 25*a-5*b+c=-3
Gleichung 1: 9*a-3*b+c=1
Gleichung 2: 25*a-5*b+c= -3
Setz c als t
9*a-3*b= 1-t
25*a-5*b= -3-t
Lösung 2 linearer Gleichung
a=t/15-7/15
b= (8*t)/15-36/15
Wird mir jedoch als falsch angezeigt, jemand eine Idee oder hat die Lösung?