Es ist

Dabei ist das letzte Gleichheitszeichen das Additionstheorem für den Tangens. Ferner wurde ausgenutzt, dass tan(pi/4) = 1.

Die Inverse der Matrix Phi wurde falsch berechnet. Es fehlt ein Faktor -0.5. Dieser fehlt dann schließlich auch im berechneten A.

/ 1  0  1 \ -1     1    / 1  0  1 \ 
| 0  1  0 |      = - *  | 0  2  0 |
\ 1  0 -1 /        2    \ 1  0 -1 /

Es geht um den Anhalteweg. Dieser setzt sich aus Reaktionsweg und Bremsweg zusammen.

Nach der Faustformel, die man in der Fahrschule lernt, beträgt alleine der Reaktionsweg bei 50km/h 15m. Nach 13m hat man also noch nicht einmal auf die Bremse getreten und fäht somit noch mit 50km/h.

Bei 230 EUR Zuverdienst beträgt der Freibetrag 126 EUR. Es werden also 104 EUR auf das ALG II angerechnet. Damit besteht ein Anspruch auf 696 EUR - 104 EUR = 592 EUR pro Monat. Mit 416 EUR wurden also pro Monat 176 EUR zu wenig gezahlt. Bei 6 Monaten macht das 1056 EUR.

Der Minijob bringt 126 EUR pro Monat mehr in die Kasse. Wenn das über Nachzahlungen laufen muss, hat man tatsächlich bis zur Nachzahlung weniger zur Verfügung. Das ist eigentlich nicht in Ordnung.

Die Laufzeit hängt natürlich stark vom verwendeten Algorithmus ab. Wenn man das ungefähr so macht

N = 50
binom = 1
for k in range(1, N):
    binom = binom * (N+1-k) // k 
    print(k, binom)

benötigt man 49 Schleifendurchläufe und in jedem Durchlauf 4 Ganzzahloperationen. Das ist nicht viel. Das dauert auf einem normalen Computer keine Sekunde (Die Ausgabe ist vermutlich langsamer als die Berechnung).

Man benötigt kein Array und die Zahlen bleiben alle weit unter n! Python (>=3) kann mit beliebig großen Ganzzahlen umgehen. Es kann aber sein, dass sehr große Zahlen die Laufzeit negativ beeinflussen.

Die Definition von f(t) sollte nicht als Gleichung auftauchen.
Löse( {$2, $3, $4}, {a, b, c} ) liefert die gewünschte Lösung.

Das Ergebnis hat mehr als 2 Nachkommastellen. In der Standardeinstellung NORM 1 zeigt der Taschenrechner das in der Exponentialschreibweise an. Man kann das auf NORM 2 umstellen. Dann passiert das erst ab 9 Nachkommastellen.

Dazu muss man zunächst so oft MODE drücken bis im Display Fix Sci Norm erscheint und anschliessend dann 3 2.

Es gibt keine positiven, ganzen a,b,c, die die Gleichungen erfüllen. Denn a,b,c wären dann wenigstens 1. Somit ist x wenigstens 73 und y wenigstens 71 und damit ist 4x^2+y^2 in jedem Fall größer als 2020.

Einrückungen sind in java egal und ein else bezieht sich immer auf das letzte if. Fügt man die (eigentlich unnötigen Klammern) hinzu und korrigiert die Formatierung, erhält man

if (a1 == true){
    if (a2 == true){
        System.out.print("Test1");
    } else {
        System.out.print("Test2");
    }
}        

Es wird also überhaupt nur etwas ausgegeben, wenn a1=true ist, was ausgegeben wird hängt dann nur noch von a2 ab.

a1=true,  a2 = true  => Test1
a1=true,  a2 = false => Test2
a1=false, a2 = true  =>
a1=false, a2 = false =>

Die Bezeichnungen p,q sind in Deutschland üblich für Hypotenusenabschnitte in einem rechtwinkligen Dreieck und h für die Höhe auf c. Allerdings zeigen die angegebenen Seitenlängen (26,10,26), dass es sich hier nicht um ein rechtwinkliges Dreieck handelt.

Wäre es ein rechtwinkliges Dreieck, könnte man mit den Kathetensätzen a^2 = c *p und b^2 = c * q, p und q berechnen und mit dem Höhensatz h^2=p*q oder mit dem Pythagoras h^2 = b^2 - q^2 die Höhe.

Bei der 3) hat der Fehlerteufel bei der Gammafunktion zugeschlagen. Es istEs muss also Gamma(3) heißen und der Exponent beim e ist -t (das sieht im Bild aus wie -1).

Bei der 2) kommt wie gewünscht 1 raus, wenn man die 2en als Quadrat interpretiert. Im Bild sind die nahezu auf einer Ebene mit den anderen Ausdrücken und könnten als "mal 2" gelesen werden.

Bei 1),4) und 5) komme ich auf die erwarteten Ergebnisse.

Entwicklung ist durchaus eine Möglichkeit. Ich komme auf eine Determinante von 21. Es bietet sich eine Entwicklung nach der dritte Spalte an, da diese zwei Nullen enthält.

|  3  1  0  4 |
| -4  2  1  6 |          | 3  1  4 |         | 3  1  4 |
|  2  1  0  3 |  = (-1)* | 2  1  3 | + (-2)* |-4  2  6 |
|  4  0  2 -1 |          | 4  0 -1 |         | 2  1  3 |


         = (-1)*[-3+0+12 - (0-2+16)] + (-2)*[18-16+12 -(18-12+16)]
         = (-1)*[9-14]               + (-2)*[14-22]
         = 5                         + 16
         = 21

Es ist Die Nullstellen des Produkts lassen sich elementar bestimmen.

Ich habe die Herleitung der Nebenbedingung nicht verstanden und halte das Endergebnis auch für falsch.

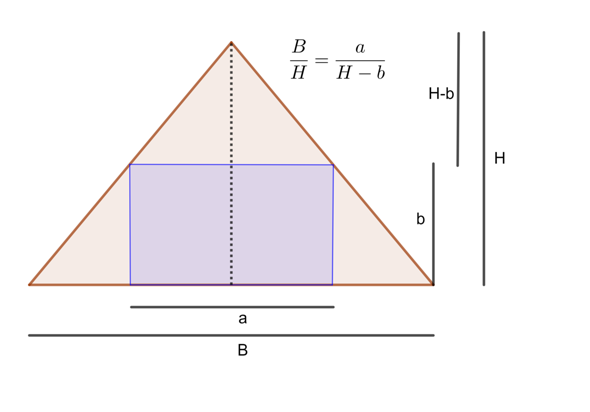
Nennen wir die Breite des Dachgeschosses B und die Höhe H, so erhält man durch Betrachten ähnlicher Dreiecke oder Strahlensatz Das kann man nach a (oder b) auflösen und in die Flächenformel einsetzen und damit die lokalen Extrema bestimmen. Als Ergebnis komme ich auf b=H/2 und a=B/2.

Man kann auch (durch Induktion) zeigen, dass a die explizite Darstellung



hat. Dann sind die Behauptungen direkter zu zeigen.

So wie f gewählt wurde, muss man zeigen, dass f(x) <= 0 für alle x >= 0.

Das kann man tun, indem man zeigt, dass f(0) <= 0 und dass f monoton fallend ist. Ersteres ist sofort ersichtlich. Um zu zeigen, dass f monoton fällt, zeigt man, dass für die Ableitung f' gilt: f'(x) <= 0. 

Die Verwirrung scheint eh schon groß zu sein. Da kann ich die Situation kaum verschlimmern, wenn ich mein Verständnis dazu auch noch kundtue. In meiner Welt gilt:

 

Allgemein ist a^-1 die Schreibweise für das Inverse von a. Was das bedeutet hängt davon ab, in welcher Struktur wir uns befinden. Ist a z.B. eine Zahl ist a^-1 der Kehrwert, ist a hingegen eine Funktion so ist a^-1 die Umkehrfunktion. Beides darf man eigentlich nur schreiben, wenn es das Inverse auch gibt.

Interessanterweise trifft man kaum Leute, die ernsthaft behaupten f^-1 sei die Abbildung, die einem x den Wert 1/f(x) zuordnet. Ist f = tan gibt es dann aber doch Diskussionen.

Der Rechner unterstützt verschiedene Rechenmodi: DEC (decimal, der normale), BIN(binär), OCT(octal) und HEX(hexadezimal). Die letzten drei unterstützen nur Rechnungen mit Ganzzahlen. Mit 2ndF und '+', '/', '*' oder '-' schaltet man zwischen diesen Modi um (dabei wird die gerade angezeigte Zahl dann auch in das entsprechende Zahlsystem umgerechnet).

Im HEX modus wird HEX angezeigt. Im DEC Modus wird das eingestellte Winkelmaß angezeigt.

Hier liegt übrigens ein Photo einer Anleitung des SC2030 von Rebell.

Die gleiche Frage wurde schon unter hilfe-bei-einer-knobelaufgabe beantwortet.

Im Prinzip genügt es die Gleichung modulo 4 zu betrachten. Denn dann schrumpft die Gleichung:

20y^2 - 19 x^2 = 2019

auf

0y^2 - 3 x^2 = 3 (mod 4) , d.h. (da -3 = 1 (mod 4))
         x^2 = 3 (mod 4)    

Quadrate sind aber entweder 0 (mod 4) oder 1 (mod 4). Also gibt es keine ganzen Zahlen, die die Ursprungsgleichung erfüllen.

Der Casio FX-991DE X ist das Luxusmodell von Casio unter den rein wissenschaftlichen Taschenrechnern. Dieser wäre noch am ehesten vergleichbar mit der EL-W506 Reihe von Sharp. Der EL-W531 ist der "kleinere" wissenschaftliche Taschenrechner von Sharp und hat deutlich weniger Funktionen.

Die "größeren" können bspw. numerisch Gleichungen lösen, numerisch integrieren und differenzieren, lineare Gleichungssystem (bis zu drei oder gar vier Variablen) lösen. Außerdem können sie Matrizen und Vektorrechnungen und haben (rudimentäre) Unterstützung für komplexe Zahlen.

Von der Funktionalität her ist der Casio FX-991DE X wohl ein wenig umfangreicher als das Sharp Gegenstück WL506. Das Bedienkonzept des Casios muss man sich aber vermutlich aneignen, wenn man Sharp gewohnt ist.

Rausgeschmissenes Geld wäre der Kauf wohl nicht.