Wann Sinus Cosinus Tangens?
Hallo zsm Wann benutze ich Sinus wann Kosin wann Tangens??
2 Antworten

Hi :)
Bei rechtwinkligen Dreiecken
Sieh dir mal das Bild im Anhang an. Dann hast du zwei Katheten und eine Hypotenuse, die dem rechten Winkel gegenüberliegt. Sagen wir, du hättest den Winkel Alpha. Das ist da der eingezeichnete Winkel.Dann ist die Kathete, die an dem Winkel liegt, die Ankathete. Die Kathete, die dem Winkel gegenüberliegt, ist die Gegenkathete.
Du verwendest diese hier wie folgt:
- sin(Alpha) = GK/H => Gegenkathete und Hypotenuse sind gegeben
- cos(Alpha) = AK/H => Ankathete und Hypotenuse sind gegeben
- tan(Alpha) = GK/AK => Ankathete und Gegenkathete sind gegeben
Nun sehen wir uns das Ganze bei allgemeinen Dreiecken an - wobei man hier den Tangens außer Acht lässt.
Beim allgemeinen Dreieck musst du drei Angaben haben, um die restlichen Größen zu bestimmen. Ich nenne dir zunächst den Sinussatz und anschließend den Kosinussatz:
sin(Alpha)/a = sin(Beta)/b = sin(Gamma)/c
=> Man muss sich dann eine der entsprechenden Gleichungen zur Hand nehmen und davon drei Dinge gegeben haben, um die vierte bestimmen zu können. Es gilt: Das Verhältnis von dem Sinus eines Winkels zu der Länge der gegenüberliegenden Seite ist im Dreieck für jeden Winkel und die jeweilige Seite immer das Gleiche.
c² = a² +b² -2ab * cos(Gamma)
b² = a² +c² -2ac * cos(Beta)
a² + b² +c² -2bc * cos(Alpha)
=> Drei Dinge davon müssen gegeben sein, man setzt ein und bestimmt durch Umstellen der entsprechenden Gleichung die gesuchte Größe.
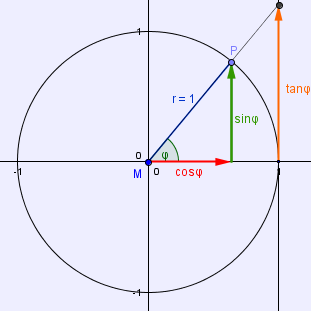
Der Tangens ist der Sinus durch den Kosinus des Winkels. Schaue in die Abbildung:
Der x.Wert des Punktes Q (so nenne ich den mal) ist 1. Der Radius wurde einfach verlängert und trifft x = 1 - das ist die Länge des Tangens. wenn du dir das genau anschaust, erkennst du eine Strahlensatzfigur, nach der gilt:
sin(Alpha)/cos(Alpha) = tan(Alpha)/1 = tan(Alpha)
q.e.d.
Ein kleiner Exkurs
Schau dir nochmal diese Gleichung an:
c² = a² +b² -2ab * cos(Gamma)
Den wichtigen und bereits bekannten Teil habe ich dir bereits markiert der kursiv gedruckte Teil ist der Satz des Pythagoras. Ich will dir eben erläutern, warum der Satz des Pythagoras ein Spezialfall des Kosinussatzes ist.
Beim Kosinussatz muss man ja zwei Seiten - hier a und b - und den davon eingeschlossenen Winkel - hier Gamma - gegeben haben. Sagen wir, Gamma sei 90°. Setzen wir ein:
c² = a² +b²-2ac * cos(90)
Schau dir nochmal unten stehende Zeichnung an. Sinus und Kosinus sind im Einheitskreis wie folgt definiert:
- Sinus: y-Wert des Punktes P
- Kosinus: x-Wert des Punktes P
Der Winkel im Einheitskreis wäre entsprechend Alpha. Nun machen wir mal Alpha = 90°, der Punkt P ist dann P(0|1). Der Kosinus des Winkels war als der xWert des Punktes P definiert, also ist dieser 0! Wenn cos(90°) = 0, dann gilt:
c² = a² +b² -2ab * 0
= a² +b² = c²
Das war jetzt der "Beweis".
Ich hoffe ich konnte helfen :))
LG ShD

google mal nach dem Einheitskreis...
http://www.semibyte.de/wp/download/graphicslib/maths/winkelfunktionen_am_einheitskreis.png
Wenn du diese Zeichnung verstehst, kannst du alle diese Funktionen selbst ableiten... zum Teil auch ohne Taschenrechner - nur mit Zirkel und Lineal!

wir sind ja nicht soweit wir berechnen nur ein dreieck und mit welcher form wir das berechnen sollen weiß ich eben nicht zB wir haben ein dreieck alpha ist sagen wir mal 30° groß die seite c ist 7cm land berechne b