Flächeinhalt & Umfang von komischen figuren
Heey , bei dieser Aufgabe habe ich noch nicht einmal ein Ansatz gefunden -.-
Tut mir leid, dass ich soviel frage. Aber ich komm einfach nicht klar..
Berechne den Flächeninhalt und den Umfang der gefärbten Fläche.
Danke..

3 Antworten
zu A) Zeichne in das Bild eine senkrechte Linie ein, so dass das Bild genau halbiert wird.
Die "Spitzen" der gefärbten Fläche, die dadurch auf der rechten Seite der Linie abgeschnitten werden, passen genau in die leeren Ecken auf der linken Seite des Bildes. der Flächeninhalt der gefärbten Fläche ist also gleich dem Inhalt der Fläche des Rechtecks links von der senkrechten Linie.
Dieses Rechteck ist ( d / 2 ) Einheiten breit und d Einheiten hoch, hat also einen Flächeninhalt A von
A= d * d / 2 = d ² / 2
Das ist somit auch der gesuchte Flächeninhalt der gefärbten Fläche.
Der Umfang U der gefärbten Fläche ist gleich der Länge zweier Halbkreisbögen mit jeweils dem Radius r = ( d / 2 ) zuzüglich den Längen der oberen und unteren Verbindung dieser Halbkreisbögen, die jeweils die Länge ( d / 2 ) = r haben.
Es ergibt sich:
U = 2 * pi * r + 2 * r = 2 * r * ( pi + 1 )
mit r = d / 2:
U = d * ( pi + 1 )
zu B) Schneide das Bild in Gedanken an der zentralen horizontalen Linie durch.
Der Teil der gefärbten Figur, der dadurch unten abgeschnitten wird (Halbkreis) passt genau in die leere Fläche unterhalb des oberen abgeschnittenen Teiles der gefärbten Fläche und ergänzt diesen zu einer Halbkreisfläche mit dem Durchmesser d.
Die Fläche dieses Halbkreises, und somit auch die gefärbte Figur, hat den Inhalt:
A = pi * ( d / 2 ) ²
Der Umfang U der gefärbten Figur ist gleich dem Umfang U1 eines Halbkreises mit dem Radius d (oberer Bogen der Figur) zuzüglich dem Umfang U2 und U 3 zweier Halbkreise jeweils mit dem Radius d / 2 (Bogen unterhalb der zentralen horizontalen Linie sowie der Bogen der leeren Fläche zwischen der Figur und der zentralen horizontalen Linie)
Es gilt also:
U = U1 + U2 + U3
mit
U1 = ( 1 / 2 ) * pi * d
U2 = U3 = ( 1 / 2 ) * pi * d / 2
also insgesamt:
U = ( 1 / 2 ) * pi * d + 2 * ( 1 /2 ) * pi * d / 2 = pi * d
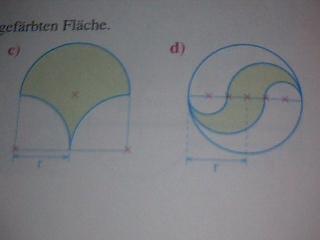
zu C) Das ist ein Rechteck ( Breite: 2 * r, Höhe: r ) mit aufgesetztem Halbkreis (Radius r). Die ausgeschnittenen Flächen bilden zusammen auch wieder einen Halbkreis mit dem Radius r.
Rechteck + Halbkreis - Halbkreis = Rechteck
Die gefärbte Fläche ist also genauso groß wie die Fläche des Rechteckes, also:
A = r * 2 r = 2 * r ²
Der Umfang ergibt sich aus der Breite des Rechteckes ( 2 * r ) + 2 mal der Höhe des Rechteckes ( r + r = 2 r ) + dem Umfang eines Halbkreises mit dem Radius r ( pi * r ), also:
U = 2 r + 2 r + pi r = ( 4 + pi ) * r
zu D) Betrachte nur die obere Hälfte des Bildes - und vergiß den äußeren Kreis!
Die gefärbte Fläche ist ein Halbkreis mit dem Radius ( 2 / 3 ) * r aus dem ein Halbkreis mit dem Radius ( 1 / 3 ) * r herausgeschnitten wurde.
Der Flächeninhalt A1 der gefärbten Fläche in der oberen Bildhälfte ist also:
A1 = pi * ( 2 / 3 ) * r - pi * ( 1 / 3 ) * r
= ( 1 / 3 ) * pi * r
Da die untere Bildhälfte symmetrisch zur oberen Bildhälfte ist, ist der Flächeninhalt der gefärbten Fläche in der unteren Bildhälfte ebenso groß, also A1 = A2
Der Flächeninhalt A der gesamten gefärbten Fläche ist daher:
A = A1 + A2 = 2 * A1 = ( 2 / 3 ) * pi * r
Der Umfang der gefärbten Fläche ist gleich dem Umfang des Kreises mit dem Radius ( 1 / 3 ) * r zuzüglich dem Umfang des Kreises mit dem Radius ( 2 / 3 ) * r, also:
U = 2 * pi * ( 1 / 3 ) * r + 2 * pi * ( 2 / 3 ) * r = 2 * pi * r
Er ist damit interessanterweise gleich dem Umfang des äußeren Kreises.
Du mußt dir die Figuren genau anschauen Auf deinen Bildern sind es meist Kreise.
Fläche:
In A hast du ein halbes Quadrat minus einen Halben Kreis Durchmesser hast du ja und einen haölben Kreis (fläche) Einfach versuchen Kreise zu finden
B ist ein halber Kreis, denn du kannst den Kleinen Kreis oben reinstecken
Versuchs mal
mein lösungsweg sind unlogisch aus ..
A= Aquadrat - ( Akreis1 - Akreis2 )
= a²- (pi *r²- ( pi* r² /2 )
= 2,2² - (pi * 1,1²- (pi * 1,1² /2)
= 4,84 - (3,8 -1,9)
= 4,84 - 1,9
= 2,94 cm²
a)
U = d * pi + d
A = d/2 * d = d^2 / 2