Ableitung von Brüchen ?
Ich komm nicht voran :( Könnt ihr mir das erklären? Wie berechnet man die Ableitung von diesem Bruch hier?
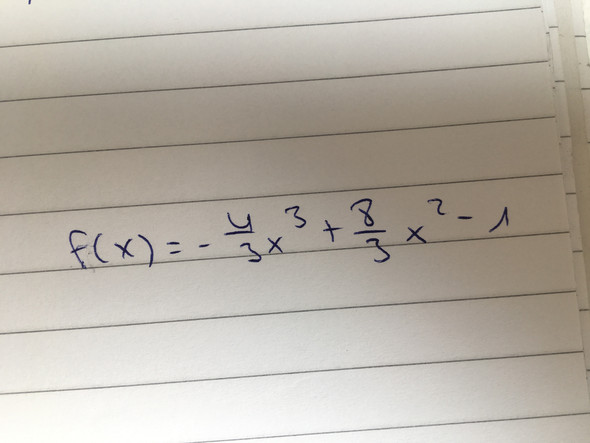
3 Antworten
genau so wie mit ganzen zahlen
denk dir doch einfach für 4/3 zb 1,333333
ist genau das gleiche, tut sich gar nix
4/3x³ sind zb abgeleitet 12/3x²
4 mal 3 und exponenten einen runter, ganz normal, nur dass du im bruch die obere zahl multiplizierst
Hallo kidtauhl1994jb
f(x) = -(4/3)x³ + (8/3)x² - 1;
f'(x) = (-4/3)*3*x² + (8/3)*2*x;
f'(x) = -4x² + (16/3)x;
Es grüßt HEWKLDOe.
Wenn man x^n ableitet, erhält man n*x^(n-1). Das gilt auch für negative n, z.B.
f(x) = 1/x² = x^(-2) hat die Ableitung f'(x) = -2x^(-3) = -2/x³;
und es gilt auch für gebrochene n, z.B.
f(x) = x^(1/2) = Wurzel(x) hat die Ableitung f'(x) = (1/2)x^(1/2-1) = (1/2)x^(-1/2) = (1/2)/x^(1/2) = 1/(2x^(1/2).
Wenn n=3 ist, also f(x) = x³, dann heißt die zugehörige Ableitung
f'(x) = 3*x^(3-1) = 3x². Daher kommt die 3. Und aus (-4/3)*3 wird -4.
Es grüßt HEWKLDOe.
Du musst den Exponenten nach vorne bringen also mittels Taschenrechner gibst du dann 3x (-4/3) usw. ein und du hast dein Ergebnis.
Ich danke ihnen vielmals aber was ist mit der 3?