Wie berechne ich diese Aufgabe physikalisch?
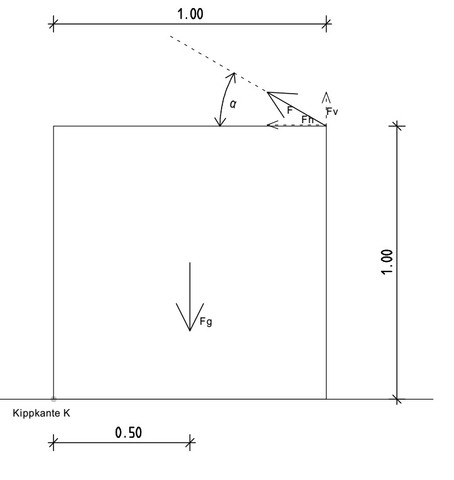
Ein Würfel aus Beton (Kantenlänge a = 1 m, Dichte ̺ = 1800 kg/m3), der sich um die linke untere Kante (K) drehen kann, soll durch ein an der oberen rechten Kante befestigtes, unter dem Winkel α = 30° gegenüber der Horizontalen gespanntes Zugseil angehoben werden. a) Wie groß ist die minimal erforderliche Zugkraft F? b) Für welchen Winkel α wird diese Zugkraft F am kleinsten, und wie groß ist sie dann?
Ich habe zwar technische Mechanik, aber weiß nicht ob das mit der selben Vorgehensweise berechnet werden soll. Ich bräuchte nur Hilfe bei den Ansätzen. Bereits im Voraus vielen Dank! :)
2 Antworten
Leider komme ich erst jetzt dazu. Viktor macht aus der Skizze ein
Geheimnis und definiert die Richtungen aus meiner Sicht nicht sinnig zur
Aufgabenstellung passend.
Daher verspätet noch meine Lösung:
Es gelten
Mstand = 1800 * g * 0,5 m
Mkipp = 1,0 m* Fh + 1,0 m* Fv
mit Fh = F * cos a
und Fv = F * sin a
Mkipp = 1, 0 * F * sin a
+ 1,0 * cos a
Ohne Einheiten
Mkipp = F * (sin a +
cos a)
Ich gehe davon aus, das die Aufgabe mit „anheben“ das
einseitige abheben des Betonwürfels gemeint ist.
Die tritt ein wenn folgende Bedingungen erfüllt sind:
-
Mkipp > MstandFh < als Reibung zwischen Boden und WürfelDas Zugseil bzw. dessen Verankerung im Beton
nicht versagt
Punkte 2 und 3 kann man nicht klären, da hierzu keine
Angaben gemacht wurden.
Aus Bedingung 1 erhält man:
1800 * g * 0,5 m = F * (sin a
+ cos a)
F = 900 g / (sin a +
cos a)
Für a= 30 °; und g =
9,81 = >
F = 900 * 9,81 / (0,5 + 0,866) = 6463 N ≈ 6 kN
Wenn nun nach der kleinsten und größten Kraft gefragt ist,
gibt es 2 Möglichkeiten:
Logik:
Das erforderliche Kippmoment ist konstant. Die kleinste Kraft braucht man wenn
der Hebelarm der Kraft am größten ist. Man muss also senkrechts zur Diagonalen
mit der Kraft angreifen, also im Winkel von 45°
.
Die größte Kraft nämlich eine unendlich große Kraft bräuchte man, wenn der
Hebelarm unendlich klein wird, also die Wirkungslinie der Kraft durch den
Kipppunkt verläuft.
Die Kraft müsste in Richtung der Diagonale angreifen, also im Winkel von 135°.
Ein
echtes Kraftmaximum kann man wie gesagt nicht angeben, da der Würfel
irgendwann anfängt zu gleiten oder schlicht das Seil abreißen wird. Ein
Winkel von 134,9° mit einer Kraft von rund 3600 kN ist daher nur
theoretisch möglich.
Das Drehmoment (Standmoment), welchem du entgegen wirken mußt ist dir ja bekannt.
Die geringste Kraft zum drehen, brauchst du, wenn du den größten "Hebelarm" zum Drehpunkt erreichst, also der Diagonalen.
Dieser ist offensichtlich bei 135 Grad der Kraftrichtung am größten.
(positive Winkel links drehend gesehen von der horiz. x-Achse)
Bei den 30 Grad bleibt der Klotz am Boden, erst ab ca 45,0001 Grad kann er bewegt werden bis 149.99. Grad.
Mach dir doch eine Skizze (wie schon empfohlen) und schau dir das an.
Korrektur
statt 149.99 Grad 314,99 Grad.
das kommt davon, weil ich mir auch keine Skizze gemacht habe, und ich bin "Spezialist" für solche Aufgaben
"Bei den 30 Grad bleibt der Klotz am Boden, erst ab ca 45,0001 Grad kann er bewegt werden bis 149.99. Grad."
??? das hätte ich gerne erklärt bekommen...
Warum sollte der Klotz nicht bewegt werden können? Es ist halt mehr Kraft notwendig. Der Klotz kann auch gekippt werden, wenn das Seil parallel zum Boden zieht.