Unser Mathprofessor hat gesagt, es gäbe nicht gleich viele reelle wie ganze Zahlen. Ist das nicht falsch?
Auch wenn das kontraintuitiv ist, gibt es doch von beiden unendlich viele?
6 Antworten

Jede natürliche Zahl N ist gleichzeitig eine ganze Zahl Z.
Also eine Zuordnung möglich.
Umgekehrt klappt es aber nicht (KEINE Bijektion? Bijektivität). So verhält es sich mit jedem weiteren Zahlenraum im Verhältnis zum anderen. Die Anzahl der vorhandenen Elemente ist hier erst mal nebensächlich, da es schlicht KEIN Gegenelement gibt. Ob nun "unendlich" was in allen Klassen zutrifft, "unterschiedlich viel" bedeuten kann ist eine andere Fragestellung.

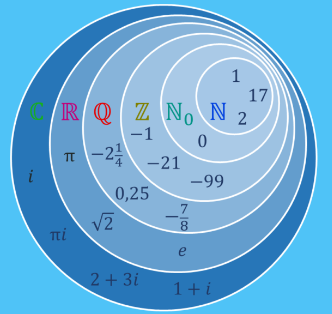

Ist vielleicht im ersten Moment kontraintuitiv - bis man versteht, dass es abzählbar unendliche Mengen (N, Z, Q) und überabzählbar unendliche Mengen (R, C, H,...) gibt.
Mehr dazu findest du zB hier

Da hat er wohl ganz offensichtlich recht.
Denn schon zwischen der Eins und der Zwei gibt es unendlich viele reelle Zahlen.
Mit besten Grüßen
gregor443

Ganz so einfach ist das nicht. Es gibt zwischen Eins und Zwei auch unendlich viele rationale Zahlen. Trotzdem gibt es genau so viele rationale wie ganze Zahlen. Es gibt aber mehr reelle als rationale Zahlen.
Und ich muss dem Fragesteller Recht geben: Intuitiv ist das nicht.

Ja, aber es geht doch um die Zuordnung, nicht? Man kann zu den unendlich vielen Zahlen zwischen eins und zwei ja unendlich viele natürliche Zahlen zuordnen ...?

N ist abzählbar, R ist überabzählbar - damit gibt es keine Bijektion zwischen den beiden Mengen und R kann als echt grösser denn N angesehen werden.

Da hat Dein Professor recht. Man unterscheidet "abzaehlbar unendlich" von "überabzaehlbar unendlich".

Ach, das ist wohl der Schlüssel und macht den Unterschied aus!!! Danke vielmals!