Die n-te Ableitung von der Sinusfunktion?
Die Ableitung von sin(x) ist cos(x) wenn ich es richtig hergeleitet habe? Habe aber nicht den Differentialquotient sondern einfach mit den Extrema und Wendepunkten gearbeitet.
Mir ist folgendes aufgefallen, die vierte Ableitung von sin(x) ist wieder der sin(x). Daraus folgt die achte Ableitung der Sinusfunktion ist wieder der Sinus selbst... usw.
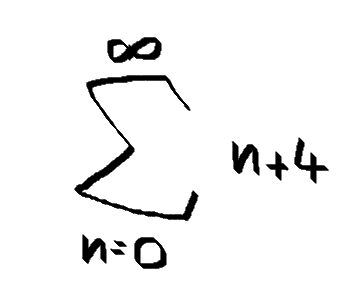
Mathematisch ausgedrückt [Siehe Bild 1], oder?
Das wäre doch dann aber weiter eine Zahlenreihe die folgendermaßen aufgebaut ist:
0,4,8,12,16,...
Geht also bis ins unendliche, man kann doch aber dann nicht sagen die Unendlichste Ableitung der Sinusfunktion ist dieser selbst.
Da doch genau solch eine Zahlenreihe ins unendliche geht:
1,2,3,4,5,6,...
Also wie sagt man das?
5 Antworten

Wieso eigentlich Reihe? Du summierst hier doch überhaupt nichts auf. Es ist lediglich eine Folge, nämlich
a_n = n•4.
Man sagt
d⁴ⁿ(sin(x))/dx⁴ⁿ = sin(x),
wobei dies genau genommen Physiker - Jargon ist, Mathematiker schreiben die Ableitungen einer Funktion f(x) lieber
f'(x), f''(x),…, f^{(n)}(x),….
als
df(x)/dx bzw. (d/dx)f(x),
(d²\dx²)f(x),
…
(dⁿ/dxⁿ)f(x)
…
,
wobei ihnen das natürlich geläufig ist.
(dⁿ/dxⁿ) für eine beliebige natürliche Zahl n ist übrigens ein Operator, der das nach x differenziert, was rechts von ihm steht.

Dein Gedankengang ist folgender:
f⁽⁰⁾(x) = sin(x)
f⁽¹⁾(x) = cos(x)
f⁽²⁾(x) = -sin(x)
f⁽³⁾(x) = -cos(x)
f⁽⁴⁾(x) = -(-sin(x)) = sin(x) = f⁽⁰⁾(x)
Deine Summe im Bild sagt jedoch etwas anderes aus.
Sie ist äquivalent zu folgendem Term:
(0+4) + (1+4) + (2+4) + (3+4) + ...
Da sie bis ins Unendliche geht, ist der Wert der Summe ∞.
Du möchtest aber folgendes ausdrücken:
f⁽ⁿ⁾(x) = f⁽⁰⁾(x) für f(x) = sin(x) und n mod 4 = 0
Ich hoffe, ich konnte dir helfen; wenn du noch Fragen hast, kommentiere einfach.
LG Willibergi

Du kannst es auch so sagen: Die (4k)-te Ableitung des Sinus ist wieder der Sinus (wobei k Element der ganzen Zahlen ist). Das heißt ist der Ableitungsgrad durch 4 teilbar, so ist es wieder der Sinus.
Da unendlich keine ganze Zahl ist, macht es auch keinen Sinn über Teilbarkeit zu reden.
Lg



Wie hast du eigentlich sin(x)' = cos(x) mit Hilfe von Extrema und Wendepunkten bewiesen?

Vielleicht noch als Ergänzung; so könntest du die n-te Ableitung allgemein berechnen:
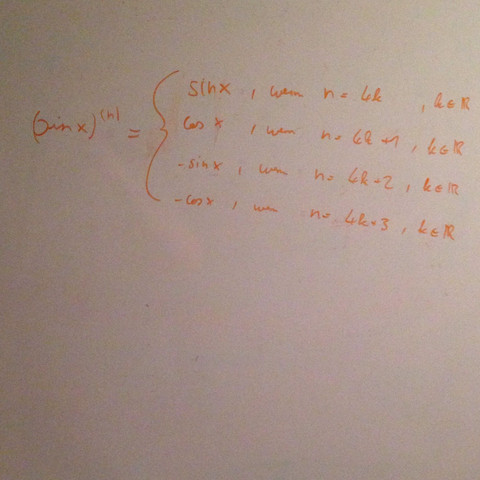


k sollte lieber element N0 sein, weil sonst lässt man auch sin(x)^(1/2) usw. zu.
Eine halbe Ableitung? wüßte jetzt nicht wie man sin(x)^(1/2) interpretieren sollte.
