Wie kann man die Koeffizienten der a,b,c,d der Funktion f(x)=ax^3+bx^2+cx+d herausfinden wenn die Nullstellen vorgegeben sind?
Hey , wäre echt nett, wenn ihr mir weiterhelfen könntet bei der Nr.13 ( wie im Bild zu sehen) :D
Gruß
Med24

5 Antworten

Können wir ja mal in der verallgemeinerten Form machen -->
u und v und w sollen die Nullstellen sein
(x - u) * (x - v) * (x - w) = ?
(x - u) * (x - v) = x ^ 2 - u * x - v * x + u * v = x ^ 2 - (u + v) * x + u * v
(x ^ 2 - (u + v) * x + u * v) * (x - w) = x ^ 3 - (u + v) * x ^ 2 + u * v * x - w * x ^ 2 + (u + v) * w * x - u * v * w
(x - u) * (x - v) * (x - w) = x ^ 3 - (u + v + w) * x ^ 2 + (u * v + (u + v) * w) * x - u * v * w
Die Koeffizienten der Funktion lassen sich nun direkt aus den Nullstellen u, v und w berechnen -->
a = 1
b = - (u + v + w)
c = (u * v + (u + v) * w)
d = - u * v * w

wegen Nullstelle setzt du für f(x) die 0 ein und für x die angegebenen Werte
a) 0 = 0+0+0+d also d=0
0 = -64a+16b-4c
0 = (4/5)³ a + (4/5)² b-4/5 c usw

d=0 hast Du korrekt bestimmt. Wenn man die Koeffizienten wirklich über vier Gleichungen bestimmen will, dann fehlt in der Tat eine Gleichung. Die Gleichungs-Koeffizientenbilanz geht nicht auf.
Nun könntest Du auf mein Ehrenwort a=1 setzen. Aber selbst dann hast Du ein homogenes Gleichungssystem, was Dir nicht Gefallen tut, dass die gesuchten Koeffizienten herauspurzeln. Versuch's mal!
Ganz anders sähe es aus, wenn tatsächlich noch eine zusätzliche Randbedingung da wäre. Zu Beispiel y(0) = 4. Dann hätten wir ein inhomogenes und damit lösbares Gleichungssystem. Und dann wäre auch a nicht mehr gleich 1.

Ich kann Deiner Logik nicht ganz zustimmen.
In einem anderen Kommentar schreibst Du: "Das a ist immer 1 in diesem speziellen Fall." Hier schreibst Du: "Und dann wäre auch a nicht mehr gleich 1." - Was soll denn nun gelten?
Ich bleibe bei meiner Behauptung: In allen Fällen der Aufgabe 13 gibt es unendlich viele Lösungen. - Bleibe ich mal bei Aufgabe a)
Rein anschaulich: Die 3 Nullstellen liegen fest. Die Frage ist also nur, wie "hoch und tief die Hügel/Täler" sind (okay, das war jetzt wenig mathematisch ausgedrückt, aber für den Fragesteller wohl anschaulich).
Und da gibt es eben unendlich viele Möglichkeiten. Ich stelle in einer neuen Antwort mal ein Bild ein.
Die Lösungen hängen tatsächlich von einer (hier fehlenden) zusätzlichen Bedingung ab. Doch f(0) = 4 zu wählen, widerspricht der Aufgabenstellung (Nullstelle bei x=0).
Um eine allgemeine Lösung zu erhalten, müsste man von der Form
f(x) = a·(x-x1)·(x-x2)·(x-x3) ausgehen. Dann hängen zum Schluss auch sämtliche Koeffizienten von a ab.

Die vierte "Gleichung" ergibt sich aus der Vorgabe, dass die Lösungen ganzzahlig sein müssen!

Für a: Nullstellen 0; -4, 4/5:
- einsetzen in f(x)=a·x³+b·x²+c·x+dI: 0 = dII: 0 = 64/125·a + 16/25·b + 4/5·cIII: 0 = -64a + 16b -4c
- Vereinfachen:II · 125 :4 → 0 = 16a+20b+25cIII :4 → 0 = -16a + 4b - c
- II + III, dann :8 → 0=2b-3c → b = 3/2 · cDaraus folgt, dass c eine gerade Zahl sein muß, damit b eine ganze Zahl ist.
- aus III:4 ergibt sich → a = b/4 - c/16Daraus ergibt sich, dass c ein Vielfaches von 16 sein muß und b ein Vielfaches von 4
- Jetzt Wertetabelle erstellen mit der Reihenfolge (wegen der oberen Gleichungen!) c … b … a → alle Tripel mit ganzen Zahlen sind Lösungen!
Ich nehme an, dass das kleinste Tripel als Lösung reicht.
Analog gehst bei den anderen Beispieln der Nummer 13 vor.
Eine eventuelle Hilfe bei der Lösung könntest du auch hier finden: http://www.wolframalpha.com/input/?i=solve+%280%3D16x%2B20y%2B25z%2C+0%3D-16x%2B4y-z%29+over+the+integers

Du schreibst die Funktion einfach als Produkt von Linearfaktoren auf. In den Linearfaktoren werden die Nullstellen direkt eingetragen. Dann multiplizierst Du alles aus und (tadaa) fertig ist die gewohnte Polynomdarstellung.
Allgemein: y = (x-x0)*(x-x1)*(x-x2) x0, x1, x2 sind die drei Nullstellen
Ausmultiplizieren kannst Du selbst.


... wobei auch b,c,d von der Wahl von a abhängen :-)
Ich erhalte also eine Funktionenschar mit dem Parameter a. Oder wähle willkürlich a=1.

Aaaaah, das a. Was machen wir mit dem a? Das a ist immer 1 in diesem speziellen Fall.
Und jetzt mach ich mir den Spaß und multiplizier das genüsslich aus:
y = x³ - (x0+x1+x2)*x² + (x0*x1 + x0*x2 + x1*x2)*x - x0*x1*x2
Herrlich, diese Symmetrien da drin!
Und jetzt setze ich die Werte ein: x0=0 x1=-4 x2=4/5
y = x³ - (0-4+4/5)x² + (0+0-4*4/5) - 0
y= x³ + 16/5*x² - 16/5*x

Ja, das ist eine gute Idee. Du erweiterst die Menge der Lösungsfunktionen. Finde ich gut.

Man darf aber nicht einfach so für a einen Wert festlegen. Die Funktionenschar wäre damit die korrekte Antwort, die man mit den Angaben berechnen kann. Aber gleichzeitig ist damit die Aufgabe nicht gelöst, weil man ja auch a bestimmen soll.

Die Funktionenschar wäre damit die korrekte Antwort
Nun ist die Frage, ob es dann noch ein "Bestimmen" ist, wenn man bestimmt, dass man sich was aussuchen darf. Die neue Rechtschreibreform macht es ja so ähnlich und erklärt dass "so genanntes" und "sogenanntes" gleichermaßen richtig ist. Die Leute dürfen sich das aussuchen. Und darum freuen wir uns über die Funktionenschar. Damit alle glücklich sind habe ich mal die Konstanten a,b,c,d neu "bestimmt".
a = k k ist frei wählbar, a ist nun "bestimmt"
b = -k*(u + v + w)
c = k*(uv + uw + vw)
d = - k*u*v*w
mit u, v, w als Nullstellen (so heißen sie bei DepravedGirl)
Hier noch ein Bildchen von der Funktionenschar:
https://dl.dropboxusercontent.com/u/22840008/Funktionenschar.png

Mögliche Lösungen für 13a).
Im Bild habe ich Werte für a (den Koeffinzienten von x³) vorgegeben.
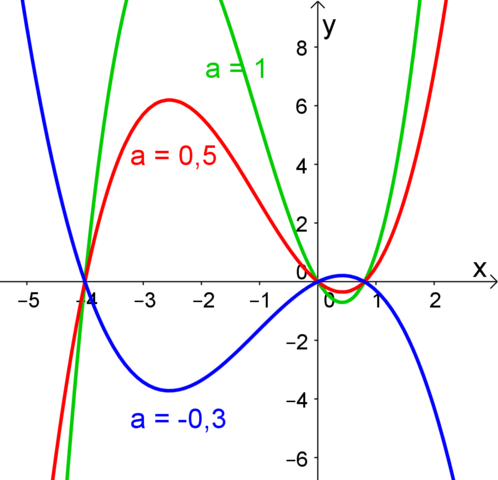
aber irgendwas haut bei der Fragestellung nicht hin;
3 Gleichungen und 4 Unbekannte.