Rechteck ABCD konstruieren, Diagonale BD & Diagonalenschnittpunkt M & 1 Punkt auf AB & 1 Punkt auf AD gegeben. Wie gehe ich vor?
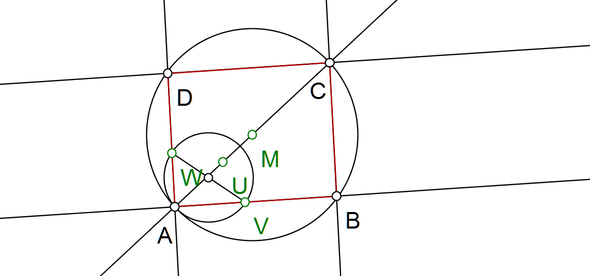
Konstruiere ein Rechteck ABCD. Diagonale BD (nicht aber Punkt B oder D) ist gegeben, Diagnoalenschnittpunkt M ist gegeben, Punkt V auf AB ist gegeben, Punkt W auf AD auch.
Ich mache einen Thaleskreis VW, Punkt A muss darauf sein. Aber wo?
Wie gehe ich vor?
4 Antworten

So gut es vom Handy aus geht:
Spiegle V an M. V' liegt auf BC. B liegt auf dem Thaleskreis über V'W und auf UM. So erhältst Du zwei Kandidaten B1, B2.
B1: Spiegelung an M liefert D1. A1 ist der Schnittpunkt von B1W und D1V, C1 dessen Spiegelung an M.
Entweder ist das Viereck A1 B1 C1 D1 entartet (Spindel) oder punktsymmetrisch mit rechtem Winkel in B1, also ein Rechteck.
B2: analog.


Hallo,
ich lade Dir eine Konstruktionsskizze hoch.
Das Ding ist durchaus aus vier Punkten zu konstruieren.
Verbinde V und W.
Schlage um die beiden einen Kreis mit der Strecke VW als Durchmesser.
Verbinde M und U durch eine Gerade.
Der Schnittpunkt der Geraden mit dem Kreis - der von den beiden Schnittpunkten, der von M weiter entfernt ist, ist A.. Weil der Kreis ein Thaleskreis ist, ist der Winkel VAW ein rechter Winkel.
Schlage um M einen Kreis mit dem Radius MA. Den Schnittpunkt der Geraden durch U und M, der nicht mit A identisch ist, nennst Du C.
Lege durch C Parallelen zu AV und AW.
Den Schnittpunkt nennst Du B.
Ziehe eine Gerade durch A und W.
Den Schnittpunkt mit der Parallele zu AV durch C nennst Du D.
Verbinde A, B, C und D.
Herzliche Grüße,
Willy

lieber Willy,
herzlichen Dank
Das wäre die Lösung, wenn V auf DC und W auf DA liegen würde, d.h. wenn die gemeinsame Ecke die aus V und W gebildet wird auf der vorgegebenen Diagonale liege würde.
Das ist aber bei dieser Problemstellung nicht der Fall. Hier ist die UM die Gerade, auf der die Diagonale BD liegt, mit dem Thaleskreis suchen wir aber Punkt A, d.h. einen Punkt von der anderen Diagonale...

Hallo,
bei Deiner Frage war ich immer davon ausgegangen, daß BD wenigstens der Länge nach bekannt ist, dann hätte man die Maße auf AC übertragen können. Später wurde mir erst klar, daß Du wirklich nur die Punkte hast.
ralphdieter hat inzwischen ja des Rätsels Lösung gepostet.
Noch eine kleine Vereinfachung vielleicht:
Spiegle V und W an M und verbinde V,W',V' und W. Um die vier Verbindungslinien schlägst Du vier Kreise (Thaleskreise).
Nun startest Du beim Schnittpunkt der Geraden durch U und M mit dem Kreis um VW' (das ist Punkt B) und ziehst von da aus eine Linie durch W', bis Du auf die Innenseite des Kreises um V'W' stößt. Von dort geht es über V' und W bis zum Thaleskreis und VW, von da aus über V nach B zurück. Die Schnittpunkte mit den Thaleskreisen sind der Reihe nach C, D und A. B hattest Du ja bereits als Startpunkt.
Habe gestern stundenlang gegrübelt und mich hinterher geärgert, daß ich meine erste Idee mit der Spiegelung nicht einfach weiterverfolgt hatte. Manchmal ist man wie vernagelt. Aber ralphdieter hat's ja dankenswerterweise gerichtet.
Herzliche Grüße,
Willy

Hallo,
fang mit den drei gegebenen Punkten an.
Verbinde V und W. Konstruiere einen Kreis k1 mit der Strecke VW als Durchmesser.. Schlage um M einen Kreis k2 mit dem Radius BD/2.
Der Schnittpunkt mit k1 ist der Eckpunkt A. Verbinde V und W mit A. Der Schnittpunkt von k2 mit der Geraden durch A und M ist Punkt C.
Lege durch C eine Parallele zu AW. Ziehe eine Gerade durch A und V. Der Schnittpunkt der Geraden mit der Parallelen durch C ist B.
Verbinde A und B.
Schlage um B einen Kreis k3 mit dem Radius BD.
Ziehe eine Gerade durch A und W.
Der Schnittpunkt dieser Geraden und k3 ist Punkt D.
Herzliche Grüße,
Willy

Ich habe keinen Punkt B und keinen Punkt D (nur die Gerade, auf der sie liegen). Daher kenne ich den Radius des Umkreises meines Rechteckes nicht...

Du hast doch die Diagonale BD. Sie ist genauso lang wie die Diagonale AC, weil es sich um ein Rechteck handelt.

Ich habe die Gerade BD, aber nicht Punkte B und D... Ich habe M, den Diagonalenschnittpunkt und U, einen Punkt der auf BD liegt...

Mein Ansatz war, dass ich Punkte E und F auf der Diagnale suche, die gleich weit von M sind... Dann verbinde ich die mit EV bzw. FW, nenne den Schnittpunkt K. Wenn ich das jetzt öfter mache, bilden die Schnittpunkte K eine Kurve, je nachdem wie weit E und F von M liegen, und A ist der Schnittpunkt der Kurve, die durch die Punkte K gebildet wird und des Thaleskreises. (der einzige Fall, wo der Winkel 90 grad ist, bzw. vielleicht gibt es 2 Fälle)
Mein Problem ist aber, dass das eine Kurve und keine Gerade ist, d.h. die Konstruktion ist immer so pi mal Daumen, aber nicht wirklich genau...

Da MA = MB ist (halbe Diagonale), schneidet ein Kreisbogen um M mit dem Radius der halben Diagonalenlänge genau deinen Thaleskreis, der übrigens eine hervorragende Idee ist, in A.
Der Rest ist Spazierengehen.

Vielen Dank fer deine Antwort. aber die Sache hat einen Haken:
ich habe D und B nicht, nur M, den Diagonalenschnittpunkt und eine Gerade durch M, auf der die Diagonale liegt.....

Was ist denn da wirklich gegeben?
Wenn das Rechteck durch Koordinaten bestimmt ist (und auch alle Punkte), so müsstest du eine Geradengleichung für die Diagonale haben,
wo nicht, muss die Länge der Diagonalen gegeben sein. Und die kannst du ja in den Zirkel nehmen.
Oder ist das Ganze ohnehin ein Vektorkonstruktion?

Es sind 4 Punkte M, U, V, W gegeben.
M ist der Diagonalenschnittpunkt unseres Rechteckes ABCD.
U liegt auf BD, d.h. U definiert die Diagonale BD, doch wir haben weder B, noch D.
V liegt auf AD
W liegt auf AB.
Es geht nicht um Vektoren oder Koordinatensystem... (haben die noch nicht gelernt)

Ja, und wie sind die Punkte gegeben? In Koordinaten?
Oder soll man sie nur einfach so aufs Papier zeichnen, dass die umgebenden Voraussetzungen gewahrt sind (ohne Vorgabe von Längen)?
U auf AB oder BD?

Als Zeichnung...
Sieht etwa aus wie ein Trapez, aber VW und MU sind nicht parallel. (aber fast)
Der Winkel zwischen VW und MU darf offensichtlich nicht 90° oder mehr sein.
Durch die 4 Punkte sind A und C definiert, aber man muss sie finden... d.h. es gibt nur 1 oder 2 Möglichkeiten für Punkt A auf dem Thaleskreis VW, wo es stimmt, dass die Geraden AV und AW die Diagonale genau so schneiden, dass M in der Mitte liegt...

Du bringst Verwirrung hinein. Jetzt ist plötzlich von einem Trapez die Rede. Vorhin war es noch ein Rechteck. Die beiden Figuren sind in keiner Weise kompatibel. Wenn man es beantworten will, muss man wissen, welchen Charakter die Figur nun hat, Auf einem Trapez könntest du niemals mit einem Punkt auf der Grundseite und einem auf dem linken (oder rechten) Schenkel einen Thaleskreis bilden.
Willst du mir die Zeichnung mal per Email schicken?
dieter01@email.de

sorry, V liegt auf Ab und W liegt auf AD, aber letztlich ist es egal...(muss man einfach B und D vertauschen)

Du hast vier Punkte M, U V W... Diese vier Punkte bilden in etwa ein Trapez, aber MU und VW sind nicht parallel (könnten es sein, aber das wäre ein Sonderfall).
Aufgrund dieser 4 Punkte soll man ein Rechteck ABCD konstruieren, so dass
M der Diagonalenschnittpunkt ist.
U auf der Diagonale BD liegt.
V auf der Geraden AB liegt.
W auf der Geraden AD liegt.
Durch diese 4 Punkte ist das Rechteck definiert (bzw. es gibt vielleicht zwei Möglichkeiten). Aber den Punkt A zu finden ist schwer...
A liegt auf dem Thaleskreis VW, da ha AV rechtwinkelig zu AW ist.
Aber wo?

Du hast mit U einen Punkt nachgereicht, den du oben nicht erwähnt hattest. Hast du noch irgendetwas anderes nicht erwähnt? Ist eventuell auch nur eine einzige Länge spezifiziert?

U definiert MU, und das ist die Gerade, auf der die Diagonale BD liegt. Ich habe erwähnt, dass die Gerade, auf der die Diagonale BD liegt bekannt ist. Das kommt auf dasselbe raus...
Nein. Wie gesagt: durch V und W (und M als diagnolenschnittpunkt und UM als Gerade, auf der Die Diagonale liegt) ist das Rechteck definiert.
A muss auf dem Thaleskreis VW liegen, und es ist der Punkt, der so ist, dass AV und AW die Diagonale gleich weit von M schneiden (da AM = MC)


Tut mir leid.
Ich habe es noch einige Male versucht. Es fehlt aber immer irgendeine weitere Größe. Nur dass A irgendein Punkt auf der Peripherie des Thaleskreises ist, reicht für die Konstruktion nicht aus. Ich sehe jedenfalls keinen Weg, da AV und AW zwar einen rechten Winkel bilden, ich aber nicht sehen kann, wie ich die Schenkel davon überzeugen kann, in gleicher Entfenung von M auf der Diagonalen aufzutreffen.
Ich habe an den Strahlensatz gedacht, aber der würde Parallelen erfordern, die ja nicht vorhanden sind.
Interessieren würde mich die Lösung schon.

Mein Ansatz war: ich suche zwei Punkte E und F auf der Diagonale, gleich weit von M, zeihe die gerade EV und FW. diese Geraden schneiden sich in einem Punkt, den ich K nenne. Wenn ich nun viele verschiedene E und F durchprobiere, ergibt sich aus den Punkten K eine Kurve, Schnittpunkt zwischen dieser Kurve und Thaleskreis ist A.
Aber das ist keine sehr genaue Methode, da die Punkte K eine Kurve und keine Gerade beschreiben (soviel ich sehen konnte).

Mit Probieren ließe sich auch von A her was machen. Aber das ist ja kein Konstruktionsprinzip. Irgendeine Angabe müsste noch her!

Nein, die Angaben reichen.... (es kann sein, dass es so 2 Rechtecke gibt, aber die Angaben reichen, um einen Punkt A genau festzulegen und alle daneben auszuschliessen). Nur kann ich ihn nicht finden...

ich dachte, dass es vielleicht etwas mit einer Drehung ist und Punkt, um den gedreht wird...
Ich habe den Original-Wortlaut der Übung in einer neuen Antwort aufgeladen...