Wie kann ich Durchmesser von einer Schlüsselweite(SW) berechnen? Die Aufgabe (7) ist im Bild vorhanden?
1 Antwort
Mit dem Pythagoras:
Schau Dir mal, z.B. oben das rechtwinklige Dreieck an, das 1/12 des Sechsecks ausmacht.
Dazu hast Du mit d/2 die senkrechte Kathete und mit D/4 die waagerechte. Die Hypotenuse ist der Radius und damit D/2.
d ist gegeben, also kannst Du mit dem Pythagoras D ausrechnen.
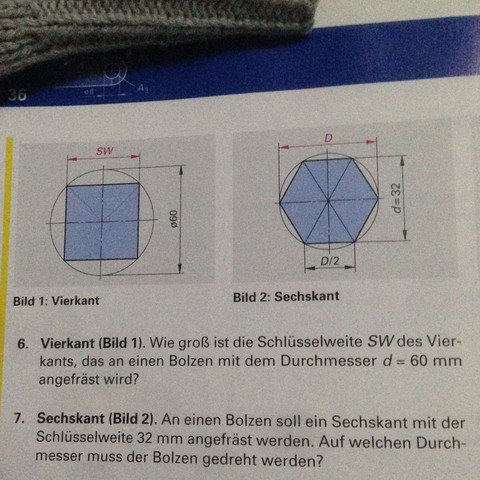
Übrigens ist die SW gegeben, Du sollst den Durchmesser des Bolzen ausrechnen.
Doch, natürlich. Du hast EINE Gleichung mit EINER Variablen (D):
(D/4)² + 16² = (D/2)²
(D/2)² - (D/4)² = 16²
(D²/4) - (D²/16) = 256
(4D² - D²)/16 = 256
3D²/16 = 256
(3/16)D² = 256
D² = 256*(16/3)
D = √(256*(16/3)) ≈ 36,95
Ich hoffe, ich habe keinen Fehler gemacht, meine letzte Mathestunde ist schon -zig Jahre her.
Und von wo holl ich die D her? d ist ja gegeben aber d ist die Höhe und mit D kann man sich die länge einer seite ausrechnen
Schau Dir mal das "Kuchenstück" unten an. Also das Dreieck, das 1/12 der Fläche ausmacht. Das ist ein Rechtwinkliges Dreieck, von dem die senkrecht stehende Kathete gleich d/2 = 16 mm ist.
Die waagerechte Kathete ist D/4 und die Hypotenuse ist D/2. Also ist der Pythagoras:
(D/4)² + 16² = (D/2)²
Und daraus kannst Du D berechnen, was gesucht ist.
Danke für die Erklärung. Ich versteh nämlich die D/2 nicht und woher kommt D/4? :/
D/2 ist doch unten eingetragen als die Länge einer Kante des Sechsecks. Und das beschriebene Dreieck hat als Kathete die Hälfte davon, also D/4.
Aber mit der (D/4)² + 16² = (D/2)² kann ich doch nicht D ausrechnen, selbst wenn ich die Formel umstelle geht das nicht oder?