PHYSIK: Achterbahn von A zu B zu C.
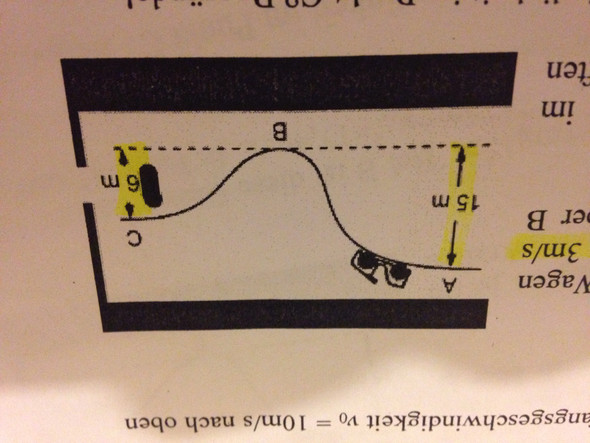
Auf einer Achterbahn bewegt sich ein Wagen (Gesamtmasse m = 700kg) mit der Geschwindigkeit 3m/s durch den Punkt A und rollt dann ohne Antrieb über B nach C. Frage: Wie groß ist die Geschwindigkeit des Wagens je im Punkt C und Punkt B, wenn man von Reibungskräften absieht? /// Die Geschwindigkeit bei Punkt B habe ich schon berechnet, es sind 17,4m/s. Aber bei dem Punkt C habe ich irgendwie Schwierigkeiten... Es wäre sehr nett wenn mir jemand die Rechenweise zeigen könnte, denn Physik ist echt mein Problemfach.
2 Antworten
Hier: musst du nur noch einsetzen, dann sollte alles passen.

Ahhh. Daaaaankeschön! :) Ich habe es jetzt verstanden. EpotB fällt ja weg, weil das Produkt davon ja 0 wäre, wenn ich das richtig verstanden habe. Nochmal vielen, lieben Dank! :)
Im Punkt C hat der Wagen kinetische und potentielle Energie. Die gesamt Energie ist natürlich auch die selbe wie im Punkt B
Daher gilt:
E_kinB+ E_potb = E_kinC +E_potC
Setz jetzt einfach alles ein und forme nach v_c um
Reicht das erstmal?
Ok sorry, dass ich nochmal störe aber ich bekomme das irgendwie nicht hin. Ich weiß nicht ob ich die falschen Zahlen einsetze oder einfach falsch umforme...
Würdest du es vielleicht mir vorrechnen, wenn es nicht zu viel verlangt ist? Wäre echt super nett und ich glaube ich verstehe es besser, wenn ich erstmal den Rechenweg vor mir liegen habe.
Ok, ich probiere es mal aus und sag Bescheid wenn ich etwas Logisches bei raus bekommen habe :) Und dankeschön!