Mathe Ableitungen - was ist mit "immer positiv" gemeint?
Hallo liebe Community,
wenn man beispielsweise die Aufgabe hat die erste und die zweite Ableitungen sind immer positiv und man dazu die passenden Graphen zeichnen soll, ist dann mit immer positiv gemeint, dass sie immer steigen oder dass sie immer im positiven Bereich. Fände es auch lieb, wenn mir jemand ein Beispiel zu der Aufgabe geben würde:) Danke schon einmal im voraus!
4 Antworten
"Im Positiven" meint sicher, immer oberhalb der X-Achse.
Und zwar nur die erste und die zweite Ableitung, nicht aber die Originalkurve selber.
Die erste Ableitung ist ja die Steigung einer Kurve.
Die zweite Ableitung ist die Steigung der Steigung.
Somit muss die Kurve steigen.
Und die Steigung muss auch steigen (zunehmen).
Fazit: Die Originalfunktion
- muss irgendwo anfangen mit einer Anfangssteigung grösser als null (also leicht nach oben zeigend). Die Originalfunktion darf selber also "unter null" sein, also auch im Negativen. Wenn sie auch null sein darf, darf sie auch horizontal beginnen.
- muss mit zunehmendem x ansteigen (erste Ableitung wird so positiv)
- darf keine konstante Steigung haben (also keine Gerade sein), sondern die Steigung muss dauernd zunehmen (und wenn die Steigung der Steigung zunimmt, ist auch die zweite Ableitung positiv).
Sowas ähnliches wie im Bild.
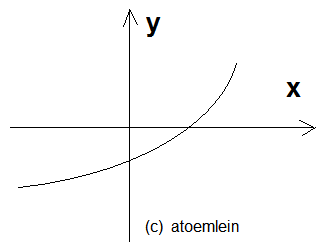
In den meisten Fällen ist damit > 0 (größer Null) gemeint.
Wenn die erste Ableitung positiv ist, steigt halt die Ursprungsfunktion. Meinst du das?
ist nicht eindeutig, was du meinst;
es gilt:
wenn f steigt, so verläuft f ' im Positiven.