Integralrechnung HILFE! wer kann diese Aufgabe lösen?
hallo zusammen, ich schreibe demnächst eine Klausur zum großen thema integralrechnung und es harpert leider bei einer aufgabe, ich hoffe, dass mir dabei vielleicht jemand helfen kann
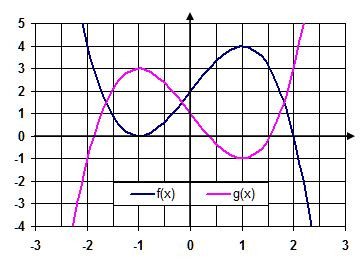
Gegeben ist die Funktion f mit der gleichung f(x)=-x^3+3x+2 a) Bestimmen sie den inhalt der Fläche zwischen dem Graphen von f und der x-achse im intervall [-2;4] b) Die Tangente im hochpunkt H (1|4) begrenzt mit dem graphen von f ein Flächenstück. Ermitteln sie die maßzahl dieser Fläche c) der graph der funktion f schließt mit dem graphen der funktion g mit der gleichung g(x)=x^3-3x+1 zwei flächenstücke ein. Bestimmen sie den Inhalt der gesamtfläche d) Die fläche, die der graph von f mit der x-achse einschließt, soll durch eine vertikale gerade mit der gleichung x=t in zwei gleich große flächenstücke geteilt werden. bestimmen sie den parameter t
bei a) habe ich -30 rausbekommen, aber denke, dass das nicht richtig ist..
3 Antworten

-30 ist bei a) richtig.
Stammfunktion:
F(x)=-1/4x^4+1.5x²+2x
F(4)=-32
F(-2)=-2
F(4)-F(-2)=-32-(-2)=-30


Nur der Vollständigkeit halber:
Die Stammfunktion ist
F(x)=-1/4x^4+1.5x²+2x +c !!
Beim bestimmten Integral (oberer Grenzwert minus unterer Grenzwert) fällt das lineare Glied (c - c) wieder heraus

TIPP : Besorge dir privat einen Graphikrechner,wei ich einen habe ,Casio.Wenn du keinen hast,kannst´e gleich einpacken !!
MERKE : Das integralzeichen S (verzerrtes S) ist der mathematische Befehl zur Aufsummierung unendlich viele kleiner Teilflächen zur Gesamtfläche A.
gegeben : f(x)=x^3+3*x + 2 Nullstelle bei x=-0,59607 keine weitere vorhanden.Integriert F(x)=1/4 *x^4 +3/2 *x^2 +2* x
1. Schritt : Nullstellen ermittel,da man nicht über Nullstellen hinweg integrieren darf.Kurvenverlauf ist schon aufgezeichnet !!t
Flächen unterhalb der x-Achse erhalten ein negatives Vorzeichen.Man muss deshalb die Einzelflächen berechnen und dann die "Beträge" der Flächen addieren.
2.Schritt : Integrieren ,Stammfunktion ermitteln ,"aufleiten" genannt
3. Schritt : Die Flächen berechnen A=obere Grenze - untere Grenze
Formel A= F(xo) - F(xu) hier x0 =obere Grenze und xu =untere Grenze
A=A1+A2 hier ist A1 die Fläche unter der x-Achse xu=- 2 u.xo=-0,59607
A2 ist die Fläche oberhalb der x-Achse xu=-0,59607 u. x0=4
A1=F(-2) - F(-,059607)=(1/4 * xo^4 +3/2 *xo^2 +2 *xo) - ( 1/4 * xu^4......)
A1=- 1,19214 - 6 =- 7,11214 Betrag also A1=7,11214 FE
Das selbe wird mit A2 gemacht und ergibt dann A=A1+A2
b. H (1/ 4) ist falsch ! f(1)= 1^3 +3*1+2= 6 also H (1/6)
Ermittlung der Tangentengleichung an der Stelle H (1/6)
yt=ft(xo)= f´(x0) * (x -xo) + f(xo) hier ist xo=1 der punkt,wo die Tangente liegt
f´(x)=3 *x^2 +3 ergibt f´(1)= 3 *1^2 +3=6
f(1)= 1^3 +3*1 +2= 6 eingesetzt
yt= 6 *(x -1)+6=6 *x - 6 +6=6* x Tangentengleichung an der Stelle x=1
Probe : yt=6 *x=6*1=6 und zum vergleich f(1)= 1^3+3 *1 +2= 6
Nun die Schnittstellen von yt und f(x) ermitteln gleichgesetz
yt=f(x) ergibt 6 *x = x^3 +3*x +2 ergibt 0=x^3 - 3 *x + 2 Nullstellen bei
x1= -2 und x2=1
Nun sollen die Flächen zwischen diesen beiden Kurven ermittelt werden
gegeben somit yt=ft(x) und f(x)
Formel A= S f(x) - g(x)
Besonderheit : Bei dieser Formel,braucht man keine Nullstellen ermittel,weil gegen den negativen Vorzeichen - g(x) die Flächen unter der x-Achse ein positives Vorzeichen erhalten und somit addiert werden.
f(x) obere Begrenzung und g(x) ist die untere Begrenzung
Besonderheit : Vertauscht man f(x) und g(x) erhält das Ergebnis ein negatives Vorzeichen.Die Vertauschung hat keinen Einfluß auf den Zahlenwert der Fläche.
Hat der Zahlenwert der Fläche ein negatives Vorzeichen,dann muss man f(x) und g(x) vertauschen.Es wechselt dann das Vorzeichen vor der Fläche.
also wäre dann A=S g(x) - f(x) hier ist S das Integralzeichen
Nun berechnen wir die Fläche zwischen F(x)=x^3+3*x+2 und yt=g(x)=6x
eingesetzt A= S (x^3 +3 *x +2) - (6 *x)=S x^3 - 3 *x +2
Integriert A=1/4 *x^4 - 3/2 *x^2 + 2 *x untere Grenze ist xu=- 2 und die obere Grenze ist xo= 1 (Dies sind die beiden Schnittpunkte von f(x) und yt=6 *x)
A= obere Genze - untere Grenze
A=F(xo) - F(xu) =(1/4 *xo^4-3/2 *xo^2 + 2 *xo) - (1/4 *xu^4-3/2 *xu^2+2xu)
A= - 6 - (0,75)= - 6,75 hier hat der Zahlenwert von A ein negatives Vorzeichen.
Man muss nun die beiden Funktionen vertauschen A =S yt - f(x)
A= S ( 6 *x) - (x^3+3 *x +2)
HINWEIS : Führe alle Schritte selber durch und kontrolliere das Ergebnis.
Achte auf Rechen-u.Tipfehler

Zu b)
Die Tangente im Hochpunkt (1|4) ist die Waagerechte y=4
Dazu habe ich den Graphen gezeichnet (Bild)
DieTangente schneidet die Funktion bei x = -2
(zur Kontrolle f(-2) = -(-8)-6+2=4)
Die Fläche, die die Tangente mit f(x) einschließt, ist
gleich der Fläche eines Rechtecks mit den
Eckpunkten (-2|0), (-2|4), (1|4) und (1|0)
minus der Fläche des Integrals f(x) im Intervall [-2;1].