Tangentgleichung und Integralrechnung bei Exponentialfunktionen?
Ich habe eine Aufgabe im Buch, wo ich die Lösung nicht verstehe.
a) Bestimmen sie die Gleichung der Tangente t an den Graphen der natürlichen Exponentialfunktion im Punkt P(2/f(2)) und berechnen sie die Nullstellen von t.
Meine Lösung: t(x) = e^2x+0,5 → kann nicht stimmen, da sie den Graphen schneidet.
b) Der Graph der natürlichen Exponentialfunktion schließt mit der Tangente im Punkt P(2/f(2)) und den Koordinatenachsen eine Fläche ein.
Berechnen sie den Inhalt dieser Fläche. → Ich verstehe die Grenzen nicht...
Vielen Dank!
3 Antworten

Hi,
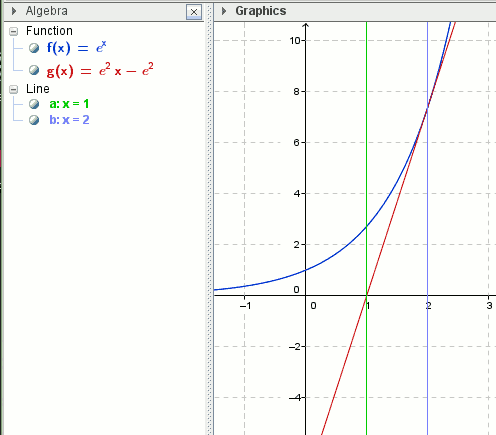
du hast dich entweder nur verrechnet oder die Gleichung der Tangente nicht richtig aufgestellt. Die Gleichung der Tangente T₂ von f(x) = eˣ in x=2 lautet:
t(x)= = f'(2)(x-2) + f(2) = e²(x-2) + e² = e² x - 2e² + e² = e²x - e²
t(x) = e²x - e²
Der Schnittpunkt von T₂ mit der x-Achse liegt bei x = 1:
t(x) = 0 <=> e²x - e² = 0 <=> e²x = e² <=> x = e² / e² = 1
b) Die Fläche F musst du in zwei Flächen F₁ und F₂ aufteilen:
F₁ = (0 bis 1) ⎰eˣ dx, F₂ = (1 bis 2) ⎰[eˣ - t(x)]dx , also F = F₁ + F₂
Gruß

vielen dank! Ich hab das jetzt verstanden. Nun habe ich aber eine neue Frage zu einer anderen Aufgabe:
a) Berechen sie die Tangente an den Graphen von f mit f(x)=o,5e^x im Punkt P(1/f(1))
Lösung: 0,5ex
b) Berechnen sie den Inhalt der Fläche, die von dem Graphen von f, der Tangente in P und der y-Achse eingeschlossen ist..

Aber wieso muss ich hier nicht aufteilen, weil man hat ja auch hier drei Graphen gegeben..

Hi musiccoolplayer,
hier brauchst du die Fläche bei der Berechnung nicht in zwei Flächen aufteilen, weil die Tangente durch den Koordinatenursprung geht.
In diesem Fall ist nur die y-Achse Begrenzung der Fläche. Zwischen 0 und 1 ist die x-Achse keine Begrenzung der Flâche, m Gegensatz zur ersten Aufgabe. (siehe meine Zeichnung oben).
Ich füge noch eine Zeichnung zu dieser Aufgabe hinzu, die du mit meiner obigen Zeichnung vergleichen kannst, dann verstehst du sofort, besser als mit Worten...
Die Grafik kann ich nicht an einen Kommentar hängen, deshalb poste ich sie in eine neue Antwort. (Antwort unten!)
Gruß

Hallo @musicoolplayer,
mit der Natürlichen Exponentialfunktion dürfte
(1) y = f(x) = e^{x}
gemeint sein, denn deren Umkehrung
(2) x = f⁻¹(y) = ln(y)
heißt ja der Natürliche Logarithmus.
Zu a)…im Punkt P(2 | f(2))…
Ich ersetze mal der Allgemeinheit halber den konkreten Wert 2 durch den Parameter (Formvariable) a. Später können wir a=2 wieder einsetzen.
Hier ist eine Anmerkung zum Sprachgebrauch angebracht:
Die Tangente berührt den Graphen in P(a | f(a)). Bei der Funktion selbst spricht man davon, dass sie in a den Wert f(a) und die Steigung f'(a) hat. Der y-Wert wird also beim Graphen, nicht aber bei der Funktion als Koordinate angesehen.
…berechnen sie die Nullstellen von t.
Eine Tangente ist eine Gerade, also der Graph einer linearen Funktion. Die hat die Form
(3) y = t(x) = mx + b
mit zwei festen Reellen Zahlen m und b, und für von 0 verschiedene Zahlen m und b hat sie genau eine Nullstelle.
Meine Lösung: t(x) = e^2x+0,5 → Kann nicht stimmen…
Schon deshalb nicht, weil ds keine Gerade und damit auch keine Tangente ist. Es ist eine Exponentialfunktion¹), und ich verstehe im Moment auch nicht, wie Du darauf kommst.
Du musst eine Funktion à la (3) finden und m und b berechnen. Dabei muss die Steigung m dieselbe sein, die auch f(x) in a hat, also f'(a). Bei der Natürlichen Exponentialfunktion ist f'(a)=f(a).
Natürlich muss die Funktion t(x) in a auch denselben Funktionswert f(a) haben, also
(4.1) t(a) = m·a + b = f(a)·a + b = f(a) ⇔ b = f(a)·(1 – a) = e^{a}·(1–a),
in a=2 also b = –e². Somit ergibt sich
(4.2) t(x) = e²·x – e² = e²·(x – 1),
und das ist 0 für x=1.
Zu b):Berechnen sie den Inhalt dieser Fläche. → Ich verstehe die Grenzen nicht...
Die linke Begrenzung ist die y-Achse x=0, die obere der Graph e^{x}.
Du musst integrieren, was bei der Natürlichen Exponentialfunktion aber einfach ist, denn wie die Ableitung f'(x) ist auch eine Stammfunktion F(x) bis auf eine Konstante C mit f(x) identisch.
Beim Ableiten gilt die Summenregel, beim Integrieren auch. Heißt: Das Integral über eine Summe und die Summe der Integrale über die Summanden ist dasselbe.
In zwei Abschnitte musst Du das Intervall [0, 2] deshalb einteilen, weil bis zur Nullstelle x=1 die untere Begrenzung durch die x-Achse gegeben ist, d.h. Du integrierst e^{x} von 0 bis 1 und erhältst natürlich
(5,1) A([0, 1]) = F(1) – F(0) = f(1) –f(0) = e¹ – e⁰ = e – 1.
Ab der Nullstelle übernimmt der Graph von t(x) die Rolle der unteren Begrenzung. Von F(2) –F(1) musst Du daher T(2)–T(1) abziehen, wobei
T(x)_[C] = e²(½·x² – x) + C
die Stammfunktionen von t(x) sind (C fällt beim Subtrahieren raus und spielt daher keine Rolle). So ergibt sich
(5.2) A([1, 2]) = F(2) – F(1) + T(1) – T(2) = e² – e – ½e² = ½e² – e.
Natürlich ist
(5.3) A([0, 2]) = A([0, 1]) + A([1, 2]) = e – 1 + ½e² – e = ½e² – 1.
Die Angaben sind ohne Gewähr. Sollte ich mich verrechnet haben, ist es Dein Job, das herauszufinden.
----
Noch eine Bemerkung zur Notation: Punkte solltest Du mit '|' oder, wenn Du partout den Slash ('/') verwenden willst, mit Leerzeichen dahinter verwenden, damit man es nicht mit einem Bruchstrich verwechseln kann.
----
¹) Die solltest Du auch eindeutiger schreiben, etwa e^{2x}+0,5, wenn der ganze Graph um 0,5 nach oben verschoben werden soll, damit man sieht, dass „+0,5“ nicht zum Exponenten gehört. Sonst könnte man das auch als e^{2x+0,5} interpretieren, und das wäre eine nach links verschobene Funktion.

a)bestimmen sie die gleichung der tangente t an den graphen der natürlichen Exponentialfunktion im Punkt P(2/f(2))
Eine Tangente ist eine Gerade, die den Graphen der Funktion f (hier die e-Funktion) in einem Punkt (hier P) berührt!
Deine Tangente ist eine e-Funktion. Sie soll aber wie gewohnt eine Gerade sein, die an der e-Funktion anliegt. Deswegen schneidet deine Funktion t sie auch.
Das ganz normale Vorgehen. Erstmal berechnen wir den Punkt komplett:
P(2|f(2))
f(x) = e^x
f(2) = e² ≈ 7,389
Jetzt fehlt uns noch die Steigung m, die wir mithilfe der Ableitungsfunktion berechnen können.
f(x) = e^x
f'(x) = e^x
f'(2) = e²
An dem Punkt P soll die Tangente also anliegen. Die Grundgleichung einer Geradengleichung lautet:
t(x) = m*x + n
Hinweis: Es werden statt n für den y-Achsenabschnitt auch noch viele andere Buchstaben wie t, c oder b genutzt. Lass dich dadurch nicht verwirren. Nun setzen wir die x und y-Koordinaten vom Punkt P in die Gleichung ein und lösen nach n auf:
e² = e² * 2 + n
e² = 2e² + n |-2e²
-e² = n
Damit ergibt sich die Tangentengleichung:
t(x) = e²x - e²
Diese liegt auch am Punkt P an.
berechnen sie die Nullstellen von t
Das bekommst du selbst hin. Die Lösung ist x=1.
b) Der Graph der natürlichen Exponentialfunktion schließt mit der Tangente im punkt P(2/f(2)) und den Koordinatenachsen eine Fläche ein,. Berechnen sie den Inhalt dieser Fläche. -> Ich verstehe die Grenzen nicht...
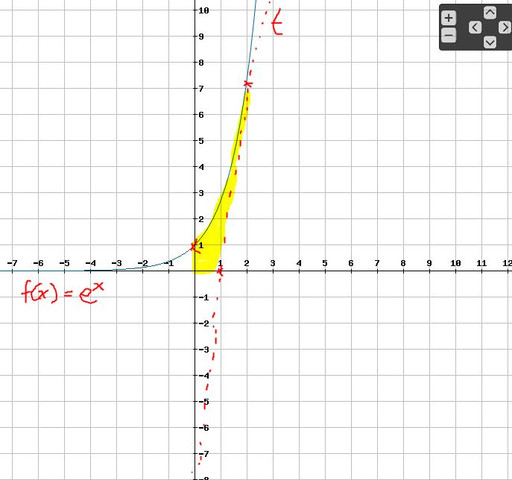
Schau dir dazu einfach meine Skizze an, die zugegebenermaßen ziemlich einfach ist ;)
Da beide Koordinatenachsen das Integral begrenzen, brauchen wir nur noch die Nullstelle von t bei x=1.. Unsere Grenzen liegen damit ab dem Ursprung, also bei U(0|0) bis zur Nullstelle bei x=1. Denke dran, beim Integral beide Funktionen mit zu nehmen. Berechne also entweder die Schnittpunkte oder mache dir eine Differenzenfunktion.
Liebe Grüße
TechnikSpezi

Vielen vielen Dank erstmal für die ausfürhliche Antwort. also a hab ich sehr gut verstanden. bei b bin ich mir noch nicht sicher, ob ich das verstanden habe. Also immer wenn ich noch eine nullstelle gegeben habe muss ich bis zu dieser integrieren und dann noch bis zu dem anderen gegebenen Punkt?

ich hab es verstanden :) aber hab nun einen neue Frage, siehe oben

Die neue Frage ist aber noch deutlich einfacher als die obere. Da liegt nämlich die Nullstelle nicht im Integrationsbereich, und die Aufteilung entfällt.
@musiccoolplayer
Für a) hast Du ja schon eine Lösung angegeben. Die war sogar noch einfacher als die andere Aufgabe a).
Zu b): Auch diese Aufgabe ist einfacher als in der Frage, denn Du kannst ohne Aufteilung
½⋅e^{x} – ½⋅e⋅x
von 0 bis 1 integrieren, also
½⋅e^{x} – ¼⋅e⋅x²
in den Grenzen 0 und 1 ausrechnen:
½(e – 1) – ¼e = ¼e – ½.