Bestimmen ganzrationaler Funktion?
Wie bestimme ich die Funktion bei
a) der Graph berührt die x-Achse im Ursprung. Die Tangente am Graphen im Punkt(3/0) ist parallel zur Geraden mit der Gleichung y=5x
b) Der Graph ist symmetrisch zur y-Achse, verläuft durch den Punkt P(0/3) und hat im Punkt Q(3/0) ein lokales Minimum
Ich wäre super dankbar wenn mir jemand helfen könnte.
3 Antworten

a)
Ansatz:
f(x) = ax^3 + bx^2 + cx + d
f'(x) = 3ax^2 + 2bx + c
Wir brauchen als 4 Bedingungen, um die 4 Unbekannten zu lösen:
f(3) = 0
f'(3) = 5
der Graph berührt die x-Achse im Ursprung:
f(0) = 0
f'(0) = 0
Also rechnen wir mal und fangen so an, dass es möglichst einfach wird und das ist besonders der Fall, wenn man mit 0 zu tun hat. Am zweitbesten wäre was mit 1.
f(0) = 0:
0 + 0 + 0 + d = 0
d = 0
f'(0) = 0
3a*0 + 2b*0 + c = 0
c = 0
Zwischenergebnis:
f(x) = ax^3 + bx^2
f'(x) = 3ax^2 + 2bx
f(3) = 0
a*3^3 + b*3^2 = 0
27a + 9b = 0 (Gl.1)
f'(3) = 3a*3^2 + 2b*3 = 5
27a + 6b = 5 (Gl.2)
Gl1 - Gl2 = 0
27a + 9b - (27a + 6b) = -5
3b = -5
b = -5/3
eingesetzt in 27a + 9b = 0:
27a - 15 = 0
27a = 15
a = 5/9
Damit lautet die Funktion:
f(x) = 5/9 x^3 - 5/3 x^2
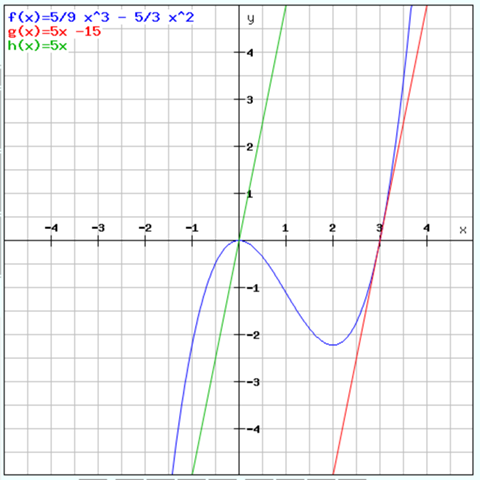
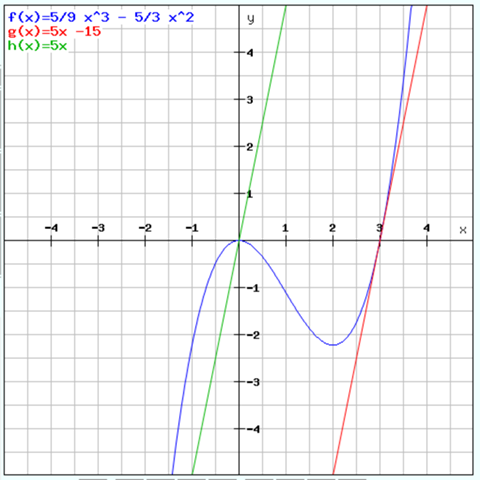

weil da steht:
der Graph berührt die x-Achse im Ursprung.
Berühren ist immer "Tangente" (sonst wäre es schneiden) und wenn die x-Achse die Tangente ist mit Steigung 0, dann ist f'(0) = 0. Der Ursprung selber hat ja x = 0


Die Parabel als Grundgleichung sollte reichen
a)
f(0) = 0
f(3) = 0
f'(3) = 5
b)
f(0) = 3
f(3) = 0
f'(3) = 0
f(x) = ax² + bx + c
f'(x) = 2ax + b
Beispiel b)
3 = a*0² + b*0 + c >>>> 3 = c
0 = a*9 + b*3 + 3
0 = 2a*3 + b
0 = 9a + 3b + 3
0 = 6a + b.......>>> -6a = b in die andere Glg einsetzen
0 = 9a + 3*(-6a) + 3
0 = 9a - 18a + 3
9a = 3
a = 1/3
-6*1/3 = b = -2
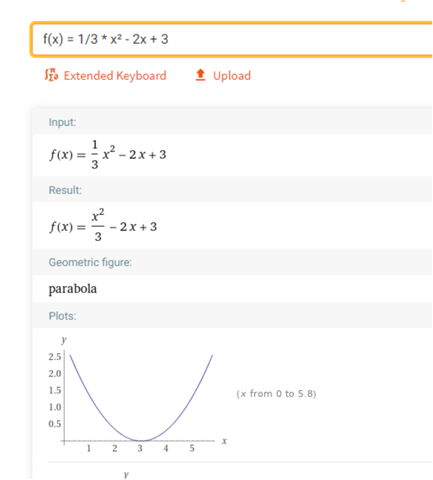
f(x) = 1/3 * x² - 2x + 3
Als Graph
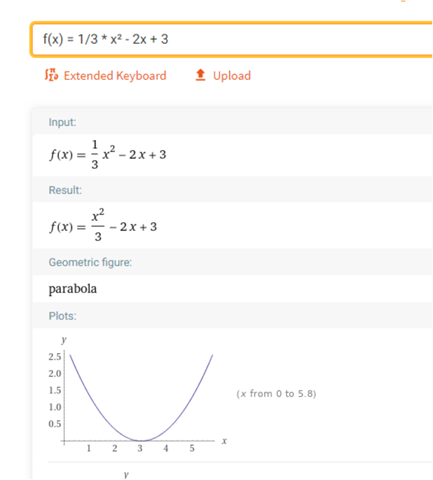
passt doch :))

Ich habe total vergessen zu erwähnen dass a eine Funktion 3. Grades und b eine Funktion 4 Grades sein soll

a)
Ursprungsberührung =>
P1(0/0)
f'(x) = 0
Tangente parallel zur gerade y(x)=5x
y'(x) = 5
P2(3/0)
b)
f(x) = f(-x)
P1(0/3)
P2(3/0)
f'(3) =0
f''(3) <0
Eine Frage hätte ich dazu noch, und zwar warum man als eine Bedingung f‘(0)=0 nehmen muss?