Hallo, ich muss für die Schule ein Lotto-Generator mit Excel erstellen.Ich muss also 6 verschiedene Zahlen aus dem Bereich 1-49 erstellen.?
5 Antworten

Für Excel lautet die Formel: =Zufallsbereich(1; 49)
Diese Formel dann einfach in 6 Zellen kopieren...

Oh ups stimmt ^^
Vielleicht kann man da noch eine Bedingungsprüfung einbauen...

ja genau irgendetwas mit =WENN aber was genau ?

Eine Idee, aber sehr unschön gelöst, wäre:
Für (A1:A6) die Formel "=Zufallsbereich(1;49)
Für B1 die Formel "=A1"
Für B2 die Formel "=(WENN(A2=A1;A2+1;A2))"
Für B3 die Formel "=(WENN(ODER(A3=A2;A3=A1);A3+1;A3))"
...
Für B6 die Formel "=(WENN(ODER(A6=A5;A6=A4;A6=A3;A6=A2;A6=A1);A6+1;A6))"
Wenn nun zufälligerweise eine Zahl doppelt vorkommt, wird die zweite davon um 1 vergrössert. Wenn jedoch 3 mal dieselbe Zahl generiert wird kommt schliesslich doch 2 mal dieselbe raus...

und dafür eine aufwändige arbeit??
nimm doch einfach: 1 - 2 - 3 - 4 - 5 - 6 und wenn du jetzt behauptest, diese zahlen würden so nie gezogen werden, dann beweise das gegenteil oder die gewißheit, dass jede andere der 14 millionen möglichen kombinationen mehr oder weniger aussicht auf erfolg hätte.


Hallo maiostr.,
YStoll hat es richtig erfasst.
Beim Lotto darf aber keine Zahl zweimal vorkommen.
Und das ist Dein Problem. Zur Lösung gibt es eine plumpe Methode:
Du fragst bei der Zweitziehung und den nachfolgenden Ziehungen einfach ab, ob die gezogene Zahl bereits in der Menge der bereits gezogenen Zahlen enthalten ist. Wenn ja, dann muss eine Sonderziehung erfolgen. Es gibt nun eine gewisse Wahrscheinlich, dass in einer Sonderziehung wieder eine bereits gezogene Zahl vorkommt. Dies nötigt Dich letztlich eine Schleife mit Endebedingung zu programmieren.
Die feine Methode:
Du beschränkst Dich auf tatsächliche 6 Ziehungen, wobei die allererste Ziehung im Bereich von 1 bis 49 unverfänglich ist und einfach abgespeichert wird.
Die Zweitziehung wird von 1 bis 48 ausgeführt. Sollte die gezogene Zahl in der Menge der bereits zuvor gezogenen Zahlen vorkommen, dann wird die gezogene Zahl einfach um den Wert 1 erhöht.
Die Drittziehung wird von 1 bis 47 ausgeführt. Sollte die gezogene Zahl in der Menge der bereits zuvor gezogenen Zahlen vorkommen, dann wird die gezogene Zahl einfach um den Wert 1 erhöht. Sollte erneut eine Übereinstimmung vorkommen, dann muss eine weitere Inkrementbildung vorgenommen werden.
Die letzte Ziehung wird von 1 bis 43 ausgeführt. Auch hier kann schlimmstenfalls eine 5fache "Umschiffung" einer vorangegangenen Ziehung nötig werden.
Dies ist übrigens einmal eine sportliche Herausforderung an alle Statistiker, ob ich mir mit diesem Algorithmus nicht eine statistische Abhängigkeit der Ziehungsergebnisse eingehandelt habe. Es könnte der Verdacht im Raum stehen, dass die "49" weniger wahrscheinliche ist als alle anderen Zahlen. Glaube ich aber nicht.
Ebenso könnte es Verklumpungseffekte durch Inkrementfolgen geben der Art 24-25-26. Glaube ich aber auch nicht.

Es könnte der Verdacht im Raum stehen, dass die "49" weniger
wahrscheinliche ist als alle anderen Zahlen. Glaube ich aber nicht.
Ebenso könnte es Verklumpungseffekte durch Inkrementfolgen geben der Art 24-25-26. Glaube ich aber auch nicht.
Leider hilft der Glaube bei mathematisch-statistischen Problemen nur wenig.
Denn beides ist der Fall, Zahlen von 44 bis 49 haben eine geringere Wahrscheinlichkeit und aufeinanderfolgene Zahlen sind wahrscheinlicher. Wobei der erste Effekt wesentlich schwerer zu spüren sein wird als der zweite.
Da die exakten Wahrscheinlichkeiten für den Fragesteller jedoch uninteressant sind, laut einem Kommentar, gehe ich nicht näher auf die Begründung für die veränderte Wahrscheinlichkeit oder eine simple eine Verbesserung des Systems von ProfFink, die diese Unstimmigkeit beheben kann, ein. Einfach weil ich mir die Arbeit nicht machen will, wenn es niemand ließt.
Sprich: Wenn es euch interessiert, kommentiert (oder besser: gebt diesem Kommentar einen Daumen hoch, sodass es in meinen Neuigkeiten auftaucht) und ich schau mal, zu wie viel Erklärung des Problems des jetzigen Vorgehens ich mich hinreißen lassen kann.

Habe nochmal ein wenig nachgedacht:
Der Algorithmus funktioniert besser, wenn man die "Gleichtreffer-Umschiffungsbedingung" wie folgt formuliert:
Wenn die gezogene Zahl gleich oder größer einer bereits gezogenen Zahl ist, dann zähle alle gezogenen Zahlen, die kleiner oder gleich der gezogenen Zahl sind und addiere die gefundene Summe zur gezogenen Zahl.
Klingt zugegebenermaßen etwas kompliziert. Eine gute Realisierung wäre mit dem Konzept einer verketteten Liste möglich, in der man das gezogene Kettenglied einfach löscht und die Ziehung dann mit der verkürzten Kette vorsetzt.

Genau da dran habe ich auch gedacht.
Auch wenn ich deine Realisierung nicht verstehe, hätte man mit diesem Ansatz wieder eine gleichmäßige Wahrscheinlichkeitsverteilung.

Ne, hab nicht mal richtiges Excel aufm PC (weil Linux) und kenne mich damit auch nicht genug aus (also mit der Linux-Version von Excel).
Außerdem würde ich Excel nicht umbedingt als "programmieren" bezeichnen :D

Nun habe ich das Problem anders gelöst und schön steht das nächste vor der Tür.
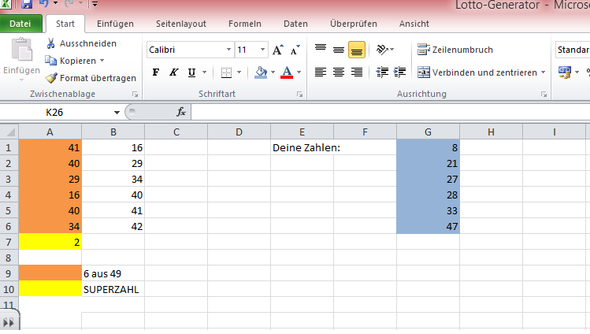
Ich habe eine Spalte (A), wo die Zahlen kreiert werden, die Spalte (B) zeigt die Zahlen mit aufsteigender Ordnung an und in der Spalte (G) habe ich dann meine eingegebene Zahlen.Ich will nun einen Vergleich darstellen, indem die Zeilen von B und G verglichen werden und dann sowas wie "Du hast 3 Zahlen getroffen" oder so

Inwiefern erstellen, programmieren oder auf nem Blatt die wahrscheinlichkeit errechnen oder was?

Das habe ich vergessen zu sagen.Ich muss das mit Excel machen, die Wahrscheinlichkeiten kann ich vernachlässigen,ich muss nur 6 verschiedene Zahlen aus 49 kreieren.
Beim Lotto darf aber keine Zahl zweimal vorkommen...