Beweis Additionstheoreme: TAN(x + y) = (TAN(x) + TAN(y)) / (1 - TAN(x)·TAN(y)) ?
Aufgabenstellung siehe Bild. Beim lernen bin ich auf folgende Aufgabe gestoßen. Leider kann ich mit der Aufgabe nichts anfangen. Es wäre sehr hilfreich, wenn jemand sich die Mühe machen würde und sie mir ausführlich vorrechnen würde. Ich bin eher so ein Typ der durch vorgerechnete Aufgaben bzw. Beispielaufgaben lernt.
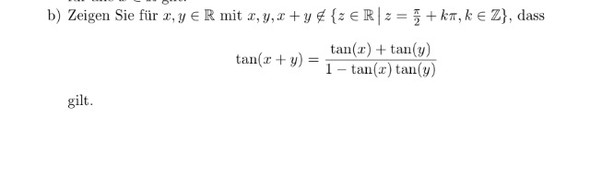
1 Antwort
tan(x+y)=sin(x+y)/cos(x+y)
Nun gilt for sin(x+y) :
sin(x+y) = sin(x)⋅* cos(y) + sin(y) * cos(x)
sin(x+y) = (cos(x) * cos(y)) * ( sin(x)⋅* cos(y) / (cos(x) * cos(y)) + sin(y) * cos(x) / (cos(x) * cos(y)))
sin(x+y) = (cos(x) * cos(y)) * ( tan(x)⋅ + tan(y) )
Nun gilt for cos(x+y) :
cos(x+y) = cos(x)⋅* cos(y) - sin(x) * sin(y)
cos(x+y) = (cos(x) * cos(y)) * ( cos(x)⋅* cos(y)/ (cos(x) * cos(y)) - sin(x) * sin(y)/ (cos(x) * cos(y)))
cos(x+y) = (cos(x) * cos(y)) * ( 1 - tan(x) * tan(y) )
d.h.
tan(x+y) = ( tan(x)⋅ + tan(y) ) / ( 1 - tan(x) * tan(y) )