Joa bei mir sind es:
1. Mathe
2. Kunst
3. IT
4. Physik
5. Sport

is bei mir nach Gewichtung geordnet

AHAHA omg Ich hatte GENAU die selbe Situation von der 7. bis mitte der 9. Klasse, als wärst du ich einfach XD ich war (und bin immernoch) der immer der jüngste in der Klasse. Jedenfalls habe ich mich damals dann immer von ihnen möglichst fern gehalten und geguckt, dass sie mich nicht sehen oder dergleichen. Als meine beiden Opponenten dann absichtig zu mir gekommen sind, um mich einfach aus spaß als Witzfigur dastehen zu lassen, hab ich das halt einfach hingenommen. Ich hab mich halt nie mit ihnen angelegt, weil ich wusste, dass mir das am ende nicht zugute kommen würde. Du darfst dir halt nicht anmerken lassen, dass du von den beiden genervt bist, denn wenn die merken, dass sie dich nicht bekommen können, hören die irgendwann von selber auf. Außerdem merken die spätestens so mitte der 10. klasse, dass das was die machen absolut nix bringt. Am ende standen die halt dumm da, weil die sich recht wenig auf das lernen konzentriert haben und dann sind die immer zu mir gerannt, weil ich immer 1er in Mathe und 2er in Physik und Chemie und Biologie hatte. Meistens habe ich die dann halt denied. Also einfach durchhalten, ich meine wie weit wollen die denn gehen?

Prekäre können auch gebildet sein

Ich lerne am liebsten mit YouTube videos und dann probier ich das selber auf m blatt papier oder aufm pc aus. Beispiel: Neues Thema in Mathe (verknüpfte Exponentialfunktionen). Ich guck mir dann videos an, wie welche Koeffizienten was bewirken und so und probier das alles dann aufm Grafikrechner aus. Dann rechne ich halt ein paar Aufgaben dazu und dann kann ich es halt. Bei so Fächern wie Deutsch oder Geschichte lese ich mir erstmal den text durch und versuche den inhalt korrekt wiederzugeben, mach ich halt so 2 oder 3 mal, sodass ich das ganze versteh und möglichst wenig auswendig lernen muss. Sollte es mal dazu kommen, dass ich auch sachen auswendig lernen muss, mach ich mir eselsbrücken, die damit im kontext stehen, sodass ich mir das gut herleiten kann.

Der Ansatz ist simpel:
a + b = 720
a - b = 86
nach a oder b auflösen, einsetzen, fertig

Wenns in der unteren Aufgabe n Halbkreis ist, dann einfach:


einfach
 und r jeweils einsetzen

A2
m gibt Auskunft über die Steigung einer linearen Funktion. je größer m, umso steiler die Funktion, je kleiner m, umso flacher die Funktion.

Wenn du die Steigung m und einen Punkt gegeben hast, brauchst du die Punktsteigungsformel zur Berechnung der Geradengleichung. Oder du bist krass und kannst das im Kopf ohne die Formel. Die Formel lautet:
wobei f(x) einfach nur sowas wie y bedeutet und xp und yp die korrespondierenden x und y Koordinaten des gegebenen Punktes sind.

Google ist dein Freund :)
Einfach googlen

Klären wir erstmal wie Maßstäbe funktionieren:

Maßstab 1 : n bedeutet, dass es auf der Abbildung kleiner ist als normal
Maßstab n : 1 bedeutet dann das es auf der Abbildung größer ist als normal
1 : 15.000 bedeutet also, dass es auf der Abbildung 15.000 mal kleiner ist als normal

wenn jz auf der Abbildung 12 cm gemessen werden, rechnest du:
12 cm * 15.000 weil das ja in echt größer ist.
Es kommen 180000 cm raus und wenn man das in m umrechnet, erhält man 1800 m und in km umgerechnet kommt man auf 1,8 km, wie der Kollege schon erwähnt hat.

Hätte ich die Aufgabe bekommen, wäre ich ehrlichgesagt als letztes auf obszönen Inhalt gekommen ich meine wen juckts wie ein Richtungsvektor heißt??? Außerdem ist das dann ja nicht deine Schuld wenn das in der Aufgabenstellung so dasteht, sag einfach du hast deinen Job gemacht und punkt. XD

15a,

 dann Determinante angucken:



jetzt den Wert für r ermitteln, bei dem D = 0 wird:

 Die Aussage ist für r = 0 wahr, also gilt:
Keine Lösung für r > 0; Eine Lösung für r = 0; Zwei Lösungen für r < 0

weil du bei D ja 0 - r rechnest, wenn r > 0 ist, dann wird das Ergebnis für D negativ, was ne negative Zahl unter der Wurzel bedeutet und DAS geht ja nicht.

____________________________________________________________________________

16,

Der Funktionsterm wurde einfach nur faktorisiert, dann wurde das ^2 durch radizieren eliminiert und nach x aufgelöst :)

Wenn damit gemeint ist, dass diese Zahl durch 3;5;6 teilbar sein soll habe ich einige möglichkeiten:

für den Natürlichen Zahlenbereich schlage ich 1 vor, da 1 durch JEDE Zahl teilbar ist und offensichtlich kleiner als 10 ist.

(was ich für 2.Klässler ehrlichgesagt ausschließe):

für den Rationalen Zahlenbereich schlage ich 0,2 und alle durch 0,2 teilbaren Zahlen vor (z.b. 0,1 ; 0,05 ...), denn:

0,2*15 = 3
0,2*25 = 5
0,2*30 = 6

wenn die Hypotenuse (die längste Seite fehlt) dann gilt:

 wobei a und b die Katheten sind

wenn eine der Katheten fehlt, dann gilt:

 c ist die hypotenuse

 <=>



<=> 

Leitkoeffizient kleiner, graph flacher

Leitkoeffizient größer, graph steiler

:D

Also bei der ersten Frage kann ich helfen:

Vereinfacht würde das so lauten:

bei der 2. bin ich leider selber unsicher :/

je größer der Koeffizient b umso mehr staucht sich die funktion.

je weiter b gegen 0 geht, desto mehr streckt sich die funktion.

ist b = 0 dann ist es einfach nur eine horizontale gerade auf der x achse

bei der a gehen wir wie folgt vor:

a=2cm das heißt die diagonale eines kästchens beträgt:

 Der Radius des großen Kreises ist also

 Denk dir noch n Dreieck mit dem großen Kreisteil hinzu, dann hast du nämlich bei genauerem hinschauen einen viertel Kreis mit Radius 2*sqrt(2(a^2)) . Davon berechnest du die Fläche mit folgender Formel:

 Dann noch die Fläche vom Dreieck:

 Dann setzt du die Werte halt ein und rechnest:

 So erhältst du den Flächeninhalt für das große Kreissegment.

jz noch die Fläche der beiden Halbkreise gleicher größe, weshalb du ganz einfach sagen kannst:

 So lautet also die Fläche der 1. Figur:



Die 2. Figur solltest du durch das Wissen, dass ich dir gegeben habe mal selbst versuchen ;)

a ist Richtig, weil du dir das Monotonieverhalten von f(x) durch f'(x) herleiten kannst. Ab dem Intervall, wo f'(x) oberhalb der X-Achse liegt, ist f(x) streng monoton steigend. liegt ein Teil von f'(x) unterhalb der X-Achse, ist der Graph von f(x) in dem Intervall streng monoton fallend.

b ist falsch, denn das muss nicht immer sein. Sehen wir uns dazu einfach dieses Bild an.

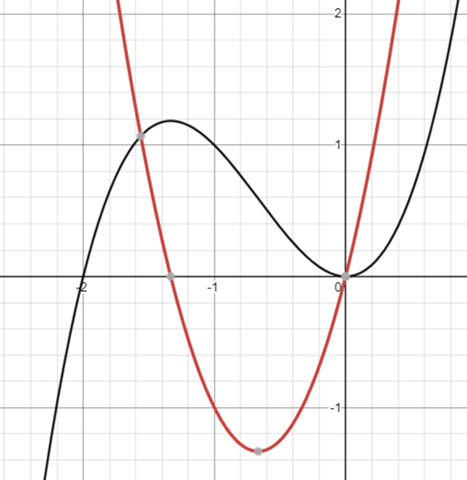
der schwarze graph ist f(x), der rote f'(x). Ab x = -4/3 ist f'(x) streng monoton steigend, f(x) ist ab x = -4/3 aber noch streng monoton fallend.