Wheatstone'sche Brückenschaltung Elektrotechnik (Erklärung)?
Bitte einfach erklären. Am besten mit Ohmschen Gesetz. Komm einfach nicht weiter.
Danke schonmal
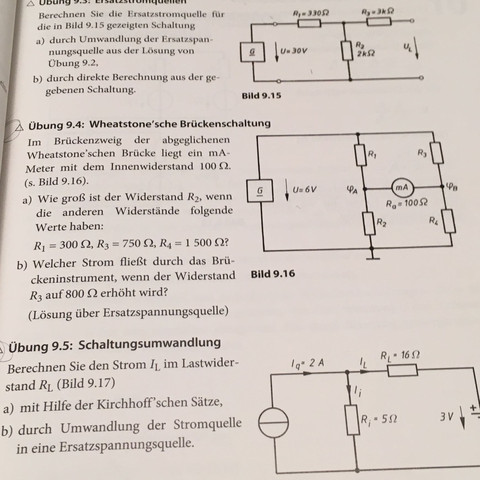
4 Antworten
zu a)
Denk Dir das mA-Meter samt Ra weg. Dann hast Du für jeden
der beiden Anschlüsse φa und φb gegen Masse einen Spannungsteiler
(1) U(φa) / U = R2 / (R1 + R2)
(2) U(φb) / U = R4 / (R3 + R4)
Wenn die Spannungen U(φa) und U(φb) gleich sind, fließt durch das
Brückenelement kein Strom, d.h. die Brücke ist abgeglichen.
U(φa) = U(φb)
R2 / (R1 + R2) = R4 / (R3 + R4)
R2R3 + R2R4 = R4R1 + R4R2 | -R4R2
R2R3 = R4R1 (damit gilt auch R2/R1 = R4/R3 oder R1/R2 = R3/R4)
R2 = R4R1/R3
R2 = 1500Ω · 300Ω / 750Ω = 600Ω
Alles richtig, was geschrieben wurde.
Einfach geht es nicht, insb. wenn man b) so verstehen will, wie es wohl gemeint ist. Allerdings ist Frage b) ein Widerspruch zur Voraussetzung der Aufgabe ("abgeglichene" Brücke) und ein Blödsinn; das interessiert in der Praxis nie.
Zu a)
Das Ohmsche Gesetz braucht man eigentlich nicht für Betrachtungen der Brücke.
Aber man muss verstehen, was ein Potential ist und was ein Spannungsteiler.
- Zwischen zwei Punkten, die auf gleichem Potential sind, kann kein Strom fliessen
- Mit jeweils zwei Widerständen zwischen Plus und Minus stellt man ein bestimmtes Potential zwischen 0 und 6 Volt ein. z.B. R1=1Teil, R2=5Teile, dann ist über R1 1Volt und über R2 5 Volt (muss zusammen 6 geben). Bezogen auf Masse (Minus) also ein Potential von 5V.
- massgeben dafür ist nur das Verhältnis der beiden Widerstände
- wenn man mit dem andern Widertandspaar das gleiche Verhältnis hinkriegt (z.B. 10/50), hat man an beiden Mittelpunkten das gleiche Potential und somit keinen Stromfluss mehr.
- In diesem Zustand gilt dann einfach R1/R2 = R3/R4
zu b)
Denk Dir einen schwarzen Kasten (Blackbox), der die ganze Brückenschaltung enthält und aus dem nur die beiden Anschlüsse φa und φb herausgeführt sind, an die das Brückeninstrument angeschlossen werden kann.
Diese Blackbox ist ein aktiver Zweipol, der gekennzeichnet ist durch seine
Leerlaufspannung Uo und den Kurzschlußstrom Ik oder durch die Leerlaufspannung Uo und seinen Innenwiderstand Ri
Es gilt Uo = Ik · Ri. Nun müssen Uo und Ri bestimmt werden.
Mit R2 = 800Ω sind U(φa) und U(φb) nicht mehr gleich
Mit den Spannungsteilergleichungen (1) und (2) zur Aufgabe a) wird:
U(φa) = U · R2 / (R1+R2) = 6V · 800Ω / (300+800)Ω = 4,36V
und
U(φb) = U · R4 / (R3+R4) = 6V · 1500Ω / (750+1500)Ω = 4,00V
Die Leerlaufspannung ist die Differenz der beiden Spannungen
Uo = U(φa) - U(φb) = 0,36V
Zur Bestimmung des Innenwiderstandes des Zweipols wird seine Spannungsquelle kurzgeschlossen und man sieht von den Klemmen aus eine Reihenschaltung von (R1 parallel R2) mit (R3 parallel R4)
Ri = R1||R2 + R3||R4
ausgerechnet Ri = 718,2Ω
Jetzt wird das Brückeninstrument (Innenwiderstand Ra) an φa und φb angeschlossen und man hat einen einfachen Stromkreis aus Uo mit
Ri in Reihe zu Ra. Der Strom durch Ra ist dann
Ia = Uo / (Ri + Ra) = 0,44mA
(Rechenfehler vorbahalten !!)
wenn die brücke abgeglichen ist , dann
R1/R2 = R3/R4
Danke, das stimmt aber kann man das auch irgendwie anders berechnen?
Ja dann danke. Und warum gilt das mit den Widerständen?