Was für Zusammenhänge haben das Gefäß und die Graphen?
Rot=erste Ableitung, Füllfunktion
2 Antworten

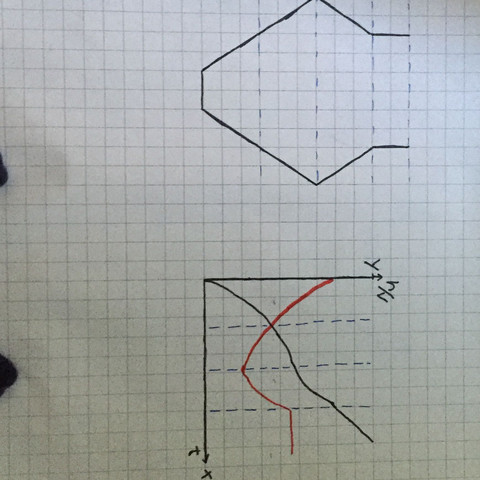
Der rote Graph zeigt die Füllgeschwindigkeit [v] in Abhängigkeit von t an.
Erst fließt das Wasser (oder irgendeine andere Flüssigkeit) schnell in das Gefäß und je breiter es wird, desto länger dauert das Auffüllen. Dann verringert sich der Durchmesser wieder und das Wasser füllt das Gefäß wieder schneller auf.
Der schwarze Graph zeigt die Füllhöhe in Abhängigkeit von t an.
Diese hängt unter anderem von [v] ab, denn sie verhält sich proportional zur Füllgeschwindigkeit. Füllt sich das Gefäß nämlich schneller (langsamer), so steigt auch die Füllhöhe schneller (langsamer);
Andersrum kann man aber auch feststellen, dass je größer (kleiner) die Änderung der Füllhöhe ist, desto schneller (langsamer) füllt sich auch das Gefäß, denn in gleicher Zeit kann vergleichsweise mehr Wasser in das Gefäß gefüllt werden.


Und in Bezug auf die Kurvendiskussion: die Änderungen von Beständen, also die Änderungsrate, ist nunmal die Ableitung der Bestandsfunktion. Hier ist f(x) also die Füllhöhe und f'(x) die Füllgeschwindigkeit.

Die schwarze Funktion gibt die Höhe der einlaufenden Flüssigkeit an.
Die rote Funktion gibt an, wie schnell die Flüssigkeit im Gefäß ansteigt. Da das Gefäß zuerst immer breiter wird, steigt die Flüssigkeit immer langsamer im Gefäß an, bis sie ab der breitesten Stelle wieder schneller steigt. Im letzten Teil steigt sie dann konstant, weil hier die Gefäßbreite gleich bleibt.
Die schwarze Funktion (Höhe der Flüssigkeit) steigt immer langsamer an, bis sie an der breitesten Stelle des Gefäßes (Wendepunkt) wieder schneller steigt, im letzten Abschnitt steigt sie konstant (hier ist die Funktion eine Gerade)
