schwieriges Integral?
Ich suche eine Stammfunktion zu:
f(x)= (ln(x))^n
Wobei n Element der natürlichen Zahlen ist, ohne der Null.
5 Antworten

Ich habe gerade den Bronstein nicht zur Hand, aber soweit ich mich erinnere, sind die Umkehrfunktionen der elementaren Funktionen (also ln, arc sin, arc cos, arc tan, ar sinh usw.) alle nicht geschlossen integrierbar.


f(x) = (ln(x))^n
Ich finde keine. Ich bin mal gespannt, ob jemand hier eine Lösung hat.
Substitution: Das Integral der äußeren Funktion von z^n * dz wäre 1/(n+1) * z^(n+1)
Würden wir aber 1/(n+1) * (ln(x)^(n+1) ableiten, so hätten wir noch den Effekt der inneren Ableitung: (n+1) * 1/(n+1) * ln(x)^n * 1/x, das letztere ist die innere Ableitung.
Die sich bildende innere Ableitung kann ich jedoch nicht eliminieren. Also F(x) = St(ln(x)^n * g(x)) mit g(x) = innere Ableitung von f(x) wäre lösbar, z.B. Stammfunktion von (ln(x)^n)*1/x.
Partiell: mit Erweiterung um Faktor 1: f(x) = 1 * (ln(x))^n
St(f(x)g(x)) = F(x)g(x) - St(F(x)g'(x))
führt zu nichts: xln(x)^n - St(x*1/x*n*ln(x)^(n-1)) = xln(x)^n - St(nln(x)^(n-1))
Es gibt aber natürlich noch die numerischen Lösungen, nach denen suchst Du aber wahrscheinlich nicht.

xln(x)^n - St(nln(x)^(n-1))
= xln(x)^n - nSt(ln(x)^(n-1))
= xln(x)^n - n*(xln(x)^(n-1) - (n-1)St(ln(x)^(n-2))
= xln(x)^n - n*(xln(x)^(n-1) - (n-1)(xln(x)^(n-2)-(n-2)St(ln(x)^(n-3))
= xln(x)^n - n*(xln(x)^(n-1) - (n-1)(xln(x)^(n-2)-(n-2)(xln(x)^(n-3)-(n-3)St(ln(x)^(n-4))
okay, kann man villeicht eine Regel draus machen
xln(x)^n - Summe(z! * x*ln(x-i)) oder ähnlich

Hallo,
geht nur rekursiv:
x*(ln(x))^n-n*Int ((ln (x))^(n-1))
Willy


Nur rekursiv?
- y₀ = x
- yₙ = x·lnⁿ⁻¹x -n·yₙ₋₁
- yₙ = x·n!·Σ (-1)ⁿ⁻ⁱ/i! lnⁱ x (i=0...n)
Sieht doch gar nicht so schlimm aus.

Hammer ! Mit Gamma-Funktion !
Ohne den Rechenweg , den die Seite https://www.integralrechner.de/ , die RayVin dankenswerterweise schon erwähnt hat , zeigt , wäre es ein endloses schreiben hier
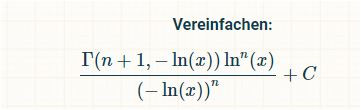
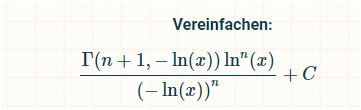

die seite hat mir ziemlich geholfen bei integralen. und ich meine jez nich einfach nur abschreiben sondern wegen dem rechwenweg (kann man anzeigen lassen)
https://www.integralrechner.de/

was ist lnt?