Rekursive Darstellung von Folgen nur mit Termdarstellung?
Halloooo. Also ich hab die Termdarstellung einer geometrischen Folge angegeben und soll jetzt die rekursive Darstellung finden. Ich blicke da nicht ganz durch und bitte um Hilfe beim Beispiel :)
xn=2^(n+1)
die Lösung ist x(n+1)= xn*2
5 Antworten

zu "blicke nicht ... durch"
§1: um durchblicken zu können, muss man auch logisch richtig schreiben.
das xn ist eine total verwirrende Schreibweise, da es auch x*n lauten könnte.
2 Schreibweisen sind logisch richtig:
a) Array: das n. Feldelement wird berechnet mit der Funktion...
x[n]=2^(n+1)=pow(2,n+1)
b) Funktionen-Schreibweise wenn man Argument n übergibt, bekommt man den Funktionswert:
f(n)=2^(n+1)=pow(2,n+1)
"REKURSIV" bedeutet nun einen Zusammenhang zwischen benachbarten a) Gliedern oder b) Funktionswerten zu finden. (Konst. Quotient bei geom. Folgen oder konst. Differenz bei arithm. Folgen)
http://www.gerdlamprecht.de/Mittelwerte.html macht das automatisch.
Da schon die Ausgangsgleichung eine Potenz ist und das Wort "geometrisch..." auftaucht, kann es nur ein konstanter Quotient sein:
x[n+1]/x[n] = 2^(n+1)/2^(n) = 2
umgestellt mal x[n]:
x[n+1] = x[n]*2 oder nach Indexverschiebung auf beiden Seiten:
x[n] = x[n-1]*2
(Nachfolger ist doppelt so groß wie Vorgänger)
Wichtig ist noch das 1. Startglied x[0], da es mit f(0) übereinstimmen muss.
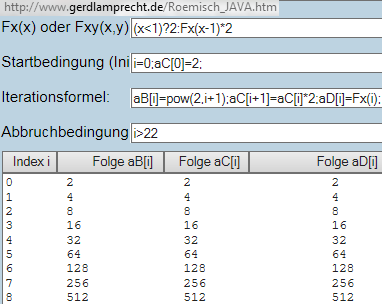
Der Iterationsrecher bietet 3 Feldvariablen an, die gleichzeitig in Spaltenform ausgegeben werden aB[...], aC[], aD[]:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#(x%3C1)?2:Fx(x-1)*2@Ni=0;@C0]=2;@N@Bi]=@P2,i+1);@Ci+1]=@Ci]*2;aD[i]=Fx(i);@Ni%3E22@N0@N0@N#
(LINK endet mit N# )
In der Informationstechnik muss man die 2 Nachteile von a) und b) kennen:
generell nur für ganzzahlige Argumente (Index) lösbar!
a) Array (Spalte aC):
- langsamer als die explizite Ausgangsfunktion
- stark ansteigender Speicherplatzbedarf (jedes Glied muss im RAM abgelegt werden)
b) rekursive Funktionen Spalte aD mit Funktion Fx(x)
- da pro Funktionsaufruf immer alle Teilergebnisse neu berechnet (Aufruf von sich selbst nur mit Argument um 1 kleiner) werden müssen und intern im STACK
abgelegt sind, ist das der langsamste aller Algorithmen!
- Speicherplatz wird zwar am Ende jeder Teilberechnung wieder freigegeben, aber während
der Berechnung kommen zu den Teilergebnissen noch die Rücksprungadressen dazu

Hallo,
die rekursive Darstellung gibt an, wie Du von einem beliebigen Folgenglied zum nächsten kommst.
Laut Potenzgesetz ist 2^(n+1) das gleiche wie 2^n*2. Um von irgendeinem Glied in der Folge zum nächsten zu kommen, mußt Du das vorhergehende einfach verdoppeln.
Also x(n+1)=x(n)*2
Beispiel:
Das dritte Glied der Folge, also x(3), ist 2^(3+1), also 2^4=16.
Das vierte ist dann das Doppelte davon, also 32.
Die kannst Du nach der anderen Formel auch direkt berechnen:
x(4)=2^(4+1)=2^5=32.
Herzliche Grüße,
Willy

x1 = 2^2 = 4
x(n+1) = 2^(n+1+1) = 2^(n+1) • 2
und da 2^(n+1) = xn folgt
x(n+1) = xn • 2

Ich sehe da keine Schwierigkeit :)
x(n) = 2^(n+1) = 2^n * 2^1 = 2 * 2^n
x(n+1) = 2 * 2^(n+1) = 2 * x(n)

Bilde x_(n+1) . Dann erkennst Du es sofort.