[Mathe] Textaufgabe mit trigonometrischen Funktionen?
Guten Abend,
ich benötige bei dieser Aufgabe noch eure Hilfe, um die Aufgabe zu verstehen. Ich freue mich sehr über eure hilfreichen Antworten. :-)
Zudem wundere ich mich, wieso das Schaubild von Ku gar nicht abgebildet ist, wie es doch eigentlich in der Aufgabe (alte Abiturabschlussprüfung) erwähnt ist.

2 Antworten
Zudem wundere ich mich, wieso das Schaubild von Ku gar nicht abgebildet ist,
Das sieht mir nach einem Fehler aus. Ohne Schaubild kann man a) nicht lösen.
b) Zunächst müssen wir v(π) bestimmen:
v(π) = a * cos π = a * (-1) = -a
Das können wir nun in u(x) einsetzen:
u(-a) = sin (π/2 * -a) + 1
und das soll = 0 sein:
sin (π/2 * -a) + 1 = 0
arcsin sin (π/2 * -a) = arcsin -1
(π/2 * -a) = 3/2 π
-a/2 = 3/2
a = -3
Leider verstehe ich es noch gar nicht, wie man die Werte für sin^(-1)(…) herausbekommt, bzw. arcsin.
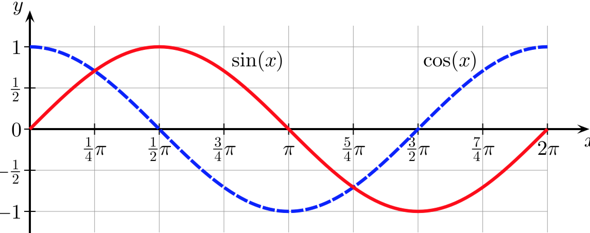
Da muss man die Kurven auswendig kennen:
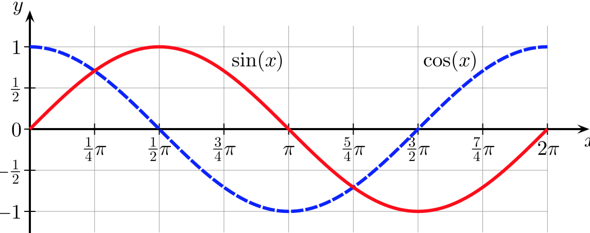
..oder sich notfalls eine schnelle Skizze machen. Insbesondere sollte man die Nullstellen und die Extrema wissen. Wenn das alles nicht hilft, hilft der Einheitskreis als Skizze weiter:
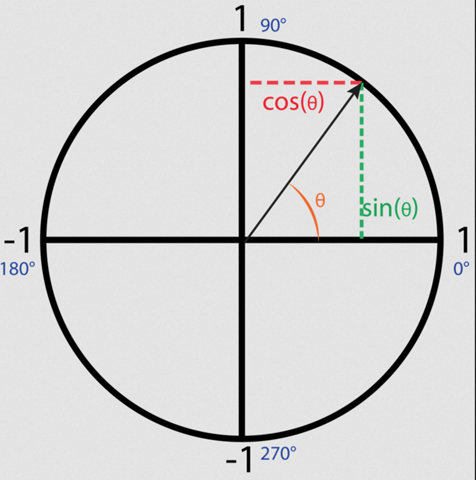
Da kann man auch leicht erkennen, dass der cosinus von π = 180° gleich -1 ist. Auch beim arcsin, arccos helfen Kurve oder Einheitskreis weiter.
Ich habe gerade im Modus RAD in denn Taschenrechner sin^(-1)(-1) eingegeben und da kommt - pi/2 raus
Taschenrechner sind so programmiert, dass der Wertebereich bei den trigonometrischen Funktionen immer zwischen - π und +π liegt. Wenn du dir den Einheitskreis aber mal anguckst, ist 90° rechtsrum dasselbe wie 270° linksrum. Die Sinus- und Cosinuswerte wiederholen sich alle 2π und -π/2 + 2π ergibt 3/2 π.
Wegen dieser Wiederholungen steht in der Aufgabe auch nicht "bestimmen Sie den Wert", sondern da steht: "bestimmen Sie einen Wert". Ein korrekter Wert wäre 3/2 π, andere korrekte Werte wären -π/2, - 5/2 π, 3,5 π etc.
Ich verstehe das leider immer noch sehr wenig, wie überhaupt der Einheitskreis aufgebaut ist
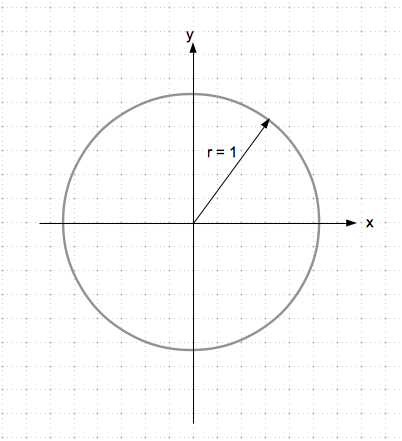
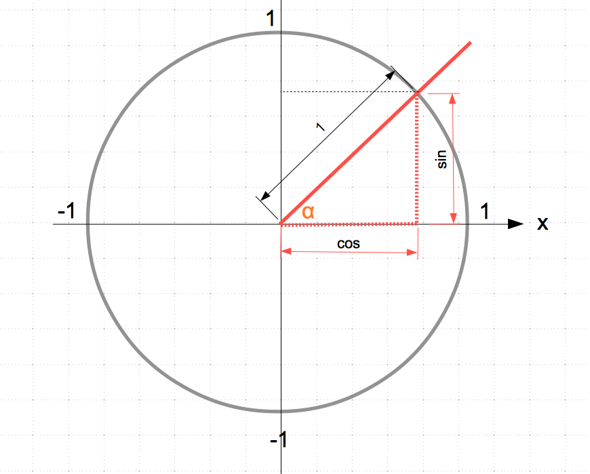
1) Du zeichnest einen Kreis mit beliebigem Durchmesser um einen Koordinatenursprung und teilst dem Radius die Größe 1 ohne Einheit zu. Durch r =1 wird der Kreis zum Einheitskreis:
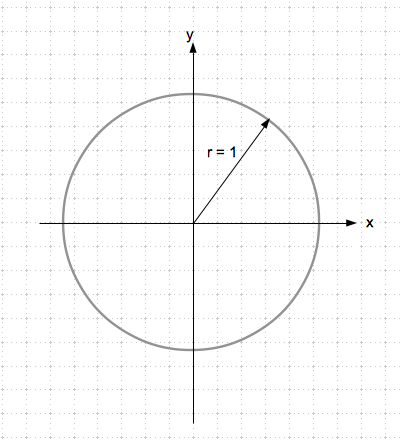
Nun zeichnest du einen Winkel α ein. Dabei beginnen wir an der x-Achse und tragen den Winkel linksherum ein. (Linksrum ist in der Mathematik eine positive Drehung).
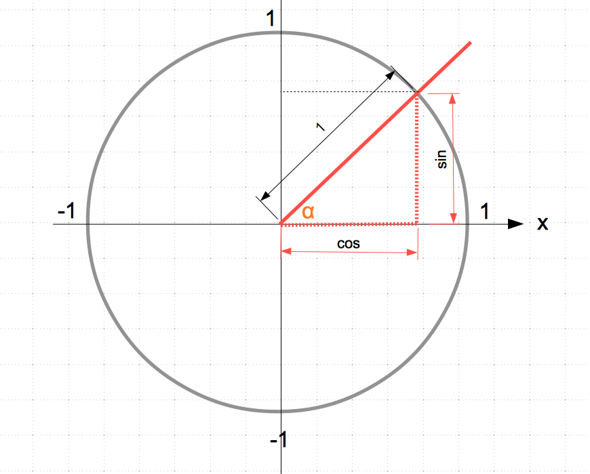
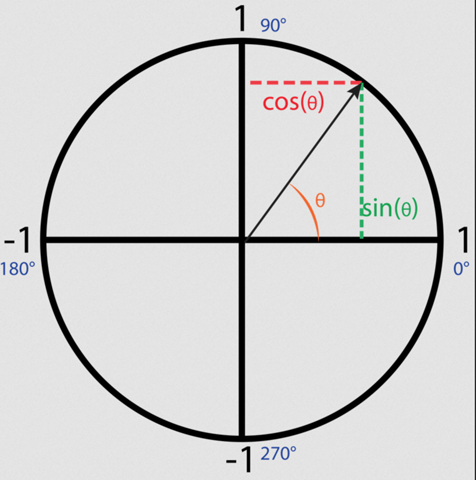
Der Winkel (rot) schneidet den Kreis und vom Schnittpunkt aus denkst du dir ein Dreieck (rot gestrichelt). Nun gilt:
sin α = Gegenkathete / Hypothenuse und da die Hypothenuse = 1 ist gilt im Einheitskreis:
sin α = Gegenkathete = y-Wert des Schnittpunktes.
Der cosinus beträgt:
cos α = Ankathete durch Hypothenuse und da die Hypothenuse = 1 ist, gilt cos α = Ankathete = x-Wert des Schnittpunktes.
Wenn man r = 1 geschickt wählt, z.B. r = 10 cm (oder notfalls r = 5 cm) , lassen sich die cosinus und sinuswerte für jeden beliebigen Winkel leicht auf 2 Stellen nach dem Komma genau an den Achsen ablesen, auch wenn man keine Hilfsmittel wie Taschenrechner, Tabellen oder Kurven zur Verfügung hat. Zirkel und Geodreieck genügen.
Der Tangens von α wäre dann Gegenkathete durch Ankathete = y/x.
Kann man solche Aufgaben wie hier nur mit dem Einheitskreis lösen?
Nein, für gerade Werte wie 0, π/2, π, 2π etc. kann man die Werte auch dadurch erhalten, dass man sich die Sinus- bzw. die Cosinuskurve qualitativ skizziert...oder die Werte auswendig lernt, was für mich die blödeste Methode wäre. Für Zwischenwert versagt die Methode aber, da gehts nur mit Taschenrechner oder Einheitskreis.
Zum Beispiel kann ich ja im Kopf lösen, dass cos(pi) = -1 ist, wenn ich mir den Verlauf der Kurve vorstelle.
Wenn das klappt ist auch gut.
Aber was ist überhaupt genau arccos? Was ist die Definition davon?
Die Gegenoperation von + ist Minus.
Die Gegenoperation von mal ist geteilt durch.
Die Gegenoperation von hoch ist Wurzel.
Die Gegenoperation von sin und cos ist arcus, welches arc abkeürzt wird oder oft auch als hoch minus 1 daherkommt.
arcsin = sin^-1
Da hat man den Funktionswert und sucht den zugehörigen Winkel.
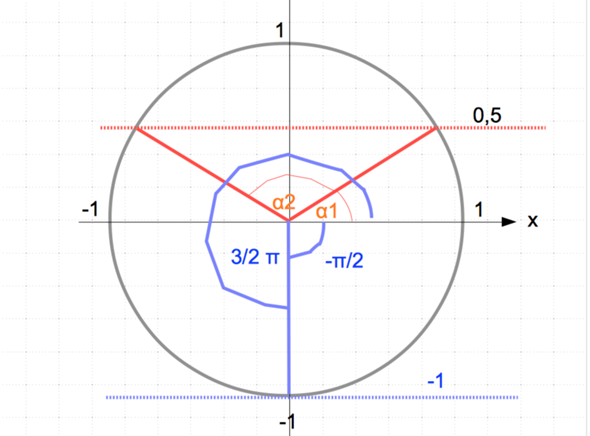
Im Einheitskreis wäre das so, dass wenn man z.B. sin^-1(0,5) sucht (rot), dass man dann bei 0,5 eine Parallele zur x-Achse zeiht und die Schnittpunkte ergeben die zugehörigen Winkel α:
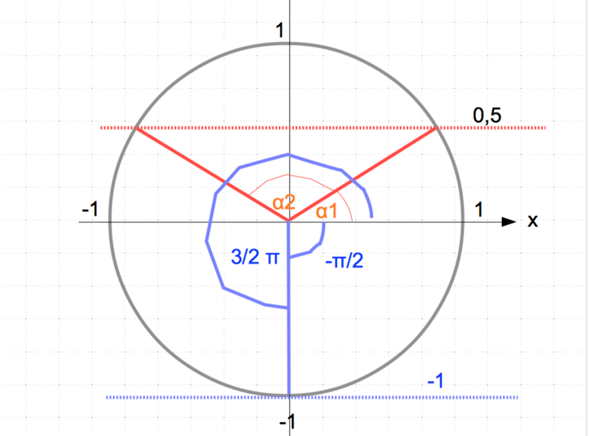
Blau: sin x = -1
x = arcsin -1 = sin^-1 (-1) = - π/2 = 3/2 π/2
Also muss ich hier zum Beispiel überlegen, bei arcsin(-1), was ich als b bei sin(b) einsstzen muss, um -1 zu erhalten, oder? Und sin(b) wird zu -1, wenn man z.B. 3/2 pi einsetzt.
Genau.
Aber wie weiß ich, ob man nun - pi/2 oder 3/2 pi einsetzen muss? Bei beiden Malen kommt ja -1 raus.
Da weder nach "allen Lösungen" oder "der Lösung", sondern nach "einer (von unendlich vielen) Lösung" gefragt ist, ist es egal, was du nimmst. Die Probe klappt mit beiden Werten.
denn ich verstehe es leider noch nicht so wirklich gut.
Vieleicht jetzt?
Muss man es am Einheitskreis machen oder kann man es sich einfach im Kopf vorstellen, wie ich es gerade gemacht habe?
Wenn du dir das im Kopf vorstellen kannst und zur richtigen Lösung kommst, ist das ok. Viele Wege führen nach Rom.
Nein, man muss π in v(x) einsetzen. Da steht ja:
u(v(π)) = 0
Also setzt man in v(x) π ein und erhält:
v(π) = a * cos π
Nun ist der cos von π aber -1 und daher erhält man als Ergebnis:
v(π) = -a
Das ist eine Abituraufgabe aus dem Teil ohne Hilfsmittel. Leider verstehe ich es noch gar nicht, wie man die Werte für sin^(-1)(…) herausbekommt, bzw. arcsin. Wie ist das System dahinter, wie weiß ich, dass sin^(-1)(-1) = - pi/2 ist? Moment mal, du bist auf 3/2 pi gekommen… Und dein Ergebnis ist auch richtig. Ich habe gerade im Modus RAD in den Taschenrechner sin^(-1)(-1) eingegeben und da kommt - pi/2 raus… Wieso komme ich da nicht auf 3/2 pi, wie du?
Ich verstehe das leider immer noch sehr wenig, wie überhaupt der Einheitskreis aufgebaut ist und was der Unterschied zwischen sinus und arcsinus, cosinus und arccosinus und tan und arctan ist und wie man das alles am Einheitskreis sehen kann.
Mit dem Einheitskreis hatte ich mich eigentlich noch nie beschäftigt.
- Kann man solche Aufgaben wie hier nur mit dem Einheitskreis lösen?
- Zum Beispiel kann ich ja im Kopf lösen, dass cos(pi) = -1 ist, wenn ich mir den Verlauf der Kurve vorstelle. Aber was ist überhaupt genau arccos? Was ist die Definition davon?
- In diesem Fall ist arccos(-1) = pi, also genau irgendwie das Gegenteil, oder?
- Also muss ich hier zum Beispiel überlegen, bei arcsin(-1), was ich als b bei sin(b) einsstzen muss, um -1 zu erhalten, oder? Und sin(b) wird zu -1, wenn man z.B. 3/2 pi einsetzt.
- Aber wie weiß ich, ob man nun - pi/2 oder 3/2 pi einsetzen muss? Bei beiden Malen kommt ja -1 raus.
Kannst du mir vielleicht helfen, dafür einen Merksatz zu schreiben, den ich mit auf eine Karteikarte schreiben kann? :-) Das würde mir unendlich helfen, denn ich verstehe es leider noch nicht so wirklich gut.
Muss man es am Einheitskreis machen oder kann man es sich einfach im Kopf vorstellen, wie ich es gerade gemacht habe?
Vielen lieben Dank für deine ganze Hilfe und deine Ergänzung! 🤩
Habe noch ein Bild eingefügt. Hatte es gaemacht, aber versäumt, einzusetzen. Vieleicht wird es dann noch klarer.
a)
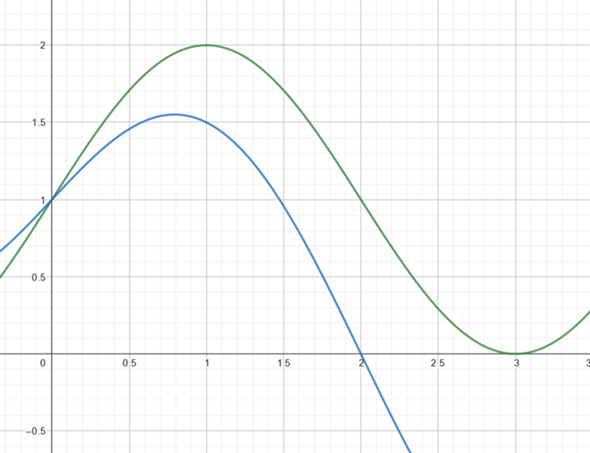
u(x) = sin(1/2*π*x) + 1 (grüne Kurve)
v(x) = sin(1/2*π*x) + 1 - 1/2*x (blaue Kurve)
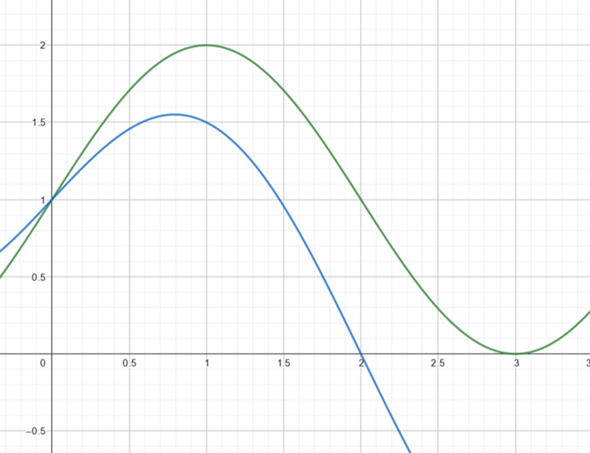
Die berechnete Fläche ist die Fläche unter der grünen Kurve im Intervall [0,3] abzüglich der Fläche unter der blauen Kurve im Intervall [0,2]
b)
v(x) = a*cos(x)
u(v(π)) = sin(1/2*π*a*cos(π)) + 1
Gesucht u(v(π)) = 0, das ist gleichwertig mit :
sin(1/2*π*a*cos(π)) = -1
sin(x) wird -1 für x = 3/2*π
also muss das Funktionsargument von sin() diesem Wert entsprechen:
1/2*π*a*cos(π) = 3/2*π
a*cos(π) = 3
Wegen cos(π) = -1 folgt a = -3
Vielen Dank für deine Antwort. :-) Schau dir sehr gerne meine neueste Frage zu Mathe an, falls du gerade Zeit und Lust hast: https://www.gutefrage.net/frage/mathe-wahrscheinlichkeit-fuer-die-mannschaften-dfb-pokal
Viele Grüße
maennlich2002
Woher weiß man, dass man x = -1 in v(x) einsetzen muss?