Jemand hilf bei Trigometrie?
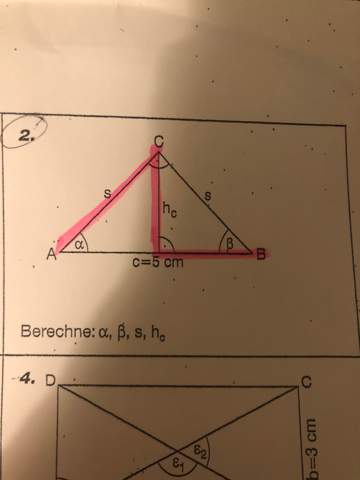
Ich muss einfach finden die Funktion für Hc,s,Alpha und Beta, und Ho aber ich kriege einfach nicht……
2 Antworten
Hallo,
bei C ist ein rechter Winkel und die Seiten, die davon ausgehen, sind gleichlang. Daher ist das Dreieck achsensymmetrisch zu h_c. Die Winkel alpha und beta sind gleich groß und betragen 45°. Die Höhe h_c ist so lang wie die Hälfte von c, also h_c=2,5cm.
s²=(½c)²+(h_c)²=2,5²cm²+2,5²cm²=12,5cm²
s=√(12,5) cm
🤓
Also du hast hier ein gleichschenkeliges Dreieck. Die Linie Hc unterteilt das Dreieck in zwei gleichgroße Dreiecke. Ober der Winkel gamma ist 90° groß und wird durch Hc durchschnitten. Du kennst also zwei Winkel in den beiden kleinen dreiecken. 1. Den Rechten Winkel 2. Den winkel oben. Die winkelsumme in einem Dreieck muss 180° betragen. Damit kanns du das ausrechnen. Wenn du alpha hast kannst du über den Sinus von alpha die Formel zu Hc umstellen. Dann über Pythagoras oder Trigonometrie s ausrechnen
Also alpha + beta + gamma = 180°
Gamma = 90° (gamma ist der Rechte winkel bei Punkt C)
=> Alpha + beta = 90°
Soweit alles klar. Aber was ist jetzt alpha oder beta? Dafür gucken wir uns die kleinen Dreiecke an.
In den kleinen Dreieck links gibt es einen Rechten Winkel, es gibt alpha und dem Winkel gamma, der durch die Linie Hc halbiert wurde.
Also alpha + 90° + 1/2 gamma = 180°
=> Alpha = 45°
So nun betrachtest du Weiter das dreieck links.
Tangenz(alpha) = Gegenkatete (hc) ÷ Ankatete (1/2 c)
=> Tan(45°) = hc / 2,5cm
So jetzt musst du die Gleichung umstellen nach hc. Dafür muliplizierst du mir 2,5cm
Also: hc = Tan(45°) × 2,5
Das gibst du in den Taschenrechner ein
Also Alpha ist nicht gefunden, soll ich Alpha + Beta + Gamma= 180 Grad, also sagen wir als Alpha oder Beta ist 90 Grad, aber was soll danach passiert…….