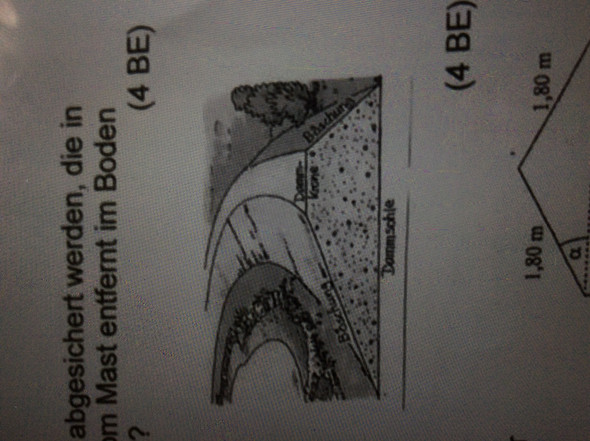
5,18m höher Schutzwall mit einer Dammkrone von 2,8m.Die Böschungen haben eine Neigung von 18 Grad und 35 Grad. Wie breit ist die Dammsohle?
5,18m höher Schutzwall mit einer Dammkrone von 2,8m.Die Böschungen haben eine Neigung von 18 Grad und 35 Grad. Wie breit ist die Dammsohle?
Kann mir das jemand mit rechendem ausrechnen komme nicht weiter
4 Antworten

Links und rechts der Dammkrone lässt sich jeweils die Höhe senkrecht einzeichnen, dadurch entstehen zwei Dreiecke in denen eine Seite (die Höhe) und Winkel (der Neigungswinkel gegen die Horizontale) bekannt sind. Dann kommt man mit den Winkelfunktionen (sin, cos, tan) weiter.

Wo liegt denn das Verständnisproblem?
Die Breite der Dammsohle meint doch die Breite des Damms unten. Wenn ich jetzt weiß wie breit die Dammkrone ist und wie Breit jeweils die Böschungen sind müsste man das doch ausrechnen können, oder?
Selber denken macht schlau ;-)

Wegen der Winkel rechnest du die beiden äußeren Teile des Damms mit dem Tangens aus. Dann brauchst du nur noch die beiden zu addieren und die Breite der Krone hinzurechnen.
Leider ist nicht alles zu sehen, aber das dürfte bereits der Weg zu deinem Ergebnis sein.
(Ich weiß nämlich nicht, was das gezeichnete, gleichschenklige Dreieck auf der rechten Seite zu bedeuten hat.)
Anmerkung: der Kontangens ist immer gleich dem Tangens des anderen Winkels an der Hypotenuse. (90° - ß)

Aber ich hab die Längen der Buchungen doch garnicht geschweigedenn die ankathete oder gegenkathete

Da Brauchst Du Winkelfunktionen (hier cotangens). Breite der Dammsohle = Ankath {Breite der "Seeseite"} (= Gegenkath {Höhe} * cot(18°)) + 2,80m + Ankath {Breite der "Landseite"} (=Höhe * cot (35°))

Haha okay cool. Ich versteh garnichts. Danke trotzdem. Aber ich habe die Länge der Böschung nicht :/ ach man i h weiß nicht was ich machen soll

Hallo Er0301,
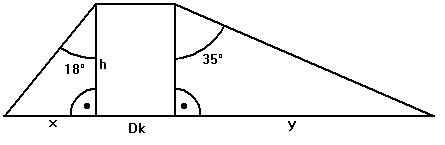
Du zerlegst den Damm in zwei Dreiecke und ein Rechteck, wie in meiner Zeichnung. Du hast in der Höhe des Damms die Ankathete der rechtwinkligen Dreiecke. Du willst die Gegenkathete wissen.
Der Tangens eines Winkels ist gleich der Gegenkathete geteilt durch die Ankathete.
Du kannst also die Formel
tan 18° = x / h | mit h multiplizieren:
x = tan 18° * h
Dasselbe machst mit y und tan 35°.
Die Dammsohle ist dann:
x + y + Dk
Gruß Friedemann
Hä? Und versteh die Aufgabe nicht kannst du es mit recheneeg machen