Hi,

Hoffe folgende Gleichungen helfen dir weiter.

Man beachte, dass lim t -> inf von exp(-jwt)*exp(-1/T*t) gegen Null strebt.

Üblicherweise werden Variablen mit Index Null für Anfangsbedingungen benutzt. Beim Zeitpunkt 0 ist die Rakete am Boden und beweget sich noch nicht, daher x0 = 0 und v0 = 0.

vs ist die Geschwindigkeit die die Rakete hat, nachdem der Treibstoff alle ist. Daher gewinnt die Rakete immernoch an Höhe obwohl der Schub nicht mehr vorhanden ist, jedoch wird sie gebremst durch die Gravitation. Dies kann man als neues Anfangswärtproblem betrachten.

Die neue Anfangsgeschwindigkeit ist vs, also v0 = vs. Die Rakete gewinnt jetzt noch solange an höhe wie ihre Geschwindigkeit grösser ist als Null, dann fängt sie wieder an zu sinken.

Also die Situation ist zweigeteilt.

1) Start vom Boden mit Anfangsgeschwindigkeit und Position gleich null.

2) Ohne Beschleunigung. Anfangsgeschwindigkeit ist gleich Endgeschwinidgkeit von 1) und Anfangsposition ist Endposition von 1) (Bei deiner Lösung wurde hier x0 = 0 gesetzt, daher ist die Endlösung h_max = Hs + Hf)

Ich vermute die Indizes s und f stehen für 'Schub' und 'Freierfall'. Hs steht nämlich für die Höhe die die Rakete mit Schub gewinnt und Hf für die ohne Schub.

Lg

8* d/dx( exp(-x) * (x-2))

Produktregel

= 8( (x-2) d/dx exp(-x) + exp(-x) d/dx (x-2))

= 8( - (x -2) exp(-x) + exp(-x))

=8( -(x-2) + 1)exp(-x)

= 8(-x + 3)exp(-x)

Hi,

1/(x-c) +[(c-x)^2 + a^2]/ (c - x)^3 =

-(c - x)^2 / (c - x )^3 + [(c-x)^2 + a^2]/ (c - x)^3

und dann der letzte schritt.

Also was gemacht wurde:

(-1) ausklammern und dann gleichnennrig machen.

Hoffe das hilft dir weiter.

Lg

Hi,

Die Permeabilität beschreibt, wie sich das Material magnetisiert wenn ein äusseres Magnetfeld angelegt wird. Eine positive Permeabilität sagt aus, dass die magnetische Dipole sich im Medium so ausrichten, dass sie das eigentliche Feld im inneren des Objektes verstärken.

Bei einem Supraleiter ist die Permeabilität 0 und dass heisst die Dipole haben sich so ausgerichtet, dass das innere des Mediums Feldfrei ist. Der sogenannte Meißner-Ochsenfeld-Effekt.

Wenn man einen Raum von magnetischen Feldern abschirmen möchte, nimmt man ein Material mit hoher Permeabilität und lenkt die Feldlinien um den Raum um. Zwar verstärkt die Magnetisierung das Feld im Inneren des Materials aber nicht draussen; die Feldlinien konzentrieren sich im Medium. Siehe Bild (https://de.wikipedia.org/wiki/Abschirmung_(Elektrotechnik))

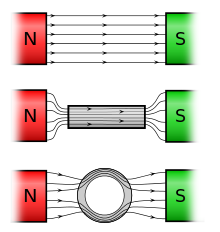
Zu deiner 2. Fragen. Ja, Stoffe mit hoher Permeabilität werden stärker von Magneten angezogen.

Hoffe das hilft dir weiter. Falls etwas unklar sein sollte oder du gerne mehr darüber wissen möchtest, lass es mich wissen.

Lg

Ich nehme an die X-Achse ist 5 ms (5 Millisekunden) pro Division.

f = 1/(2.5*10^-3 s) = 400 Hz oder 0.4 kHz.

Lg

Hallo

Wie wäre es zum Beispiel, wenn du über 'Digitale Doktoren' schreibst? Verbindet sehr aktuelle Themen wie Big Data, Machine Learning mit volkswirtschaftlichen Themen wie Ärztemangel.

Lg

Hi,

Beim Fadenpendel ist die Federkraft abhängig vom Gewicht und beim Federpendel spielt nur die Auslenkung eine Rolle.

F_Feder = k_f*x(t)

k_f: Federkonstante

x(t): Auslenkung

F_Faden = m*g*sin(phi(t))

m: Masse

g: Erdbeschleunigung

phi(t): Winkelauslenkung

Stellt man jetzt beide Bewegungsgleichungen (2. Newton Gesetz) auf, stellt man fest, dass beim Fadenpendel sich die Masse kürzt, jedoch nicht beim Federpendel.

m*a(t) = k_f*x(t) => a(t) = - k_f/m * x(t)

a(t): Beschleunigung

m*l*alpha(t) = - m*g*sin(phi(t)) => alpha(t) = - g/l*sin(phi(t))

alpha(t): Winkelbeschleunigung

l: Länge des Fadens

Hoffe das hilft dir weiter.

Lg