Wieso erfolgt bei der Tritation ein plötzlicher pH-Sprung?
Und wieso ist dieser Sprung bei der Titration einer schwachen Säure mit einer starken Base bzw. einer schwachen Base mit einer starken Säure nicht so groß? Liegt es daran, dass z.B. bei einer starken Säure (und schwachen Base) sich die Lösung mit H30+ Ionen anreichert, da ja die starke Säure auch mit dem Wasser zu Hydronium Ionen reagiert?
3 Antworten

Nehmen wir an, Du titrierst eine Säure mit einer Base (z.B. Essigsäure mit NaOH).
Am Anfang der Titration ist die Lösung sauer, am Ende basisch. Also muß sich der pH-Wert wohl verändern. Die Frage ist nur, macht er das kontinuierlich oder sprunghaft. Beides ist möglich, je nachdem, wie die Details bei der Säure liegen.
(α) Irgendwann im Lauf der Titration muß es einen Moment geben, wo Säure und Anion in ähnlichem Mengen vorliegen (bei mehrbasigen Säuren gibt es für jede Dissoziationsstufe einen solchen Moment). Dann wissen wir aber, daß (1) die Lösung einen pH ungefähr dem pKₐ hat und (2) die Pufferkapazität hoch ist, also sich der pH nicht sehr ändert, daß also die Titrationskurve in diesem Bereich flach sein muß.
(β) An den Äquivalenzpunkten ist es tendenziell umgekehrt: Idealisiert hat man da nur eine einzige Spezies in der Lösung, z.B. HPO₄²⁻ aber kaum H₂PO₄⁻ oder PO₄³⁻. In einer solchen Lösung ist die Pufferkapazität klein (außer, ihr pH ist knapp am Rand, also entweder knapp an 0 oder knapp an 14), also steigt der pH mit Zugabe der Maßlösung steil an.
Das Argument α ist zwingend: Diese Plateaus muß es in der Tritrationskurve geben, wenn die pKₐ-Wert komisch liegen, dann werden sie ein bißchen rumgeschoben aber sie sind immer da. Argument β ist dagegen nicht zwingend sondern nur plausibel. Nicht jeder Äquivalenzpunkt muß einen pH-Sprung haben, denn der Sprung könnte von der Pufferkapazität des Wassers (bei extremen pH-Werten) oder von anderen Dissoziationsgleichgewichten anderer Stufen (bei ähnlichen pKₐ-Werten) verdeckt sein.
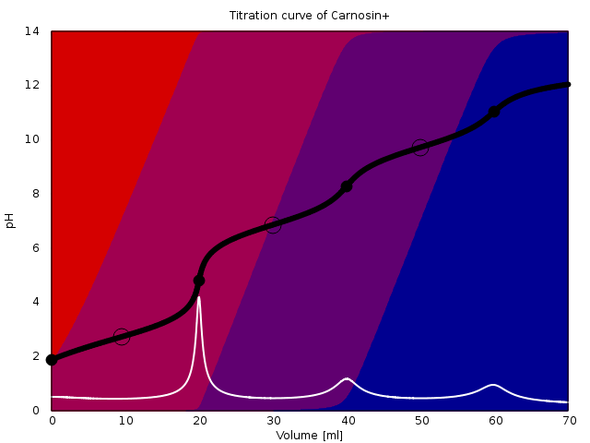
An die Antwort hänge ich ein paar Titrationskurven an, die verdeutlichen sollen, welche Variationen da insgesamt möglich sind. In jedem Fall werden 20 ml einer 0.1 mol/l Lösung einer Säure mit 0.1 mol/l NaOH titriert. Der Äquivalenzpunkt ist also bei 20 ml, und im Fall von mehrbasigen Säuren folgen die weiteren bei 40 bzw. 60 ml. Die Hintergrundfarben geben die Gleichgewichtsanteile der einzelnen Spezies der Säure an: Rot ist die freie Säure, blau die vollständig deprotonierte Form, und wenn notwendig gibt es noch Violettöne dazwischen. Äquivalenzpunkte sind mit einem fetten Kreis und Pufferpunkte (1:1-Verhältnis) mit einem leeren Kreis gekennzeichnet.
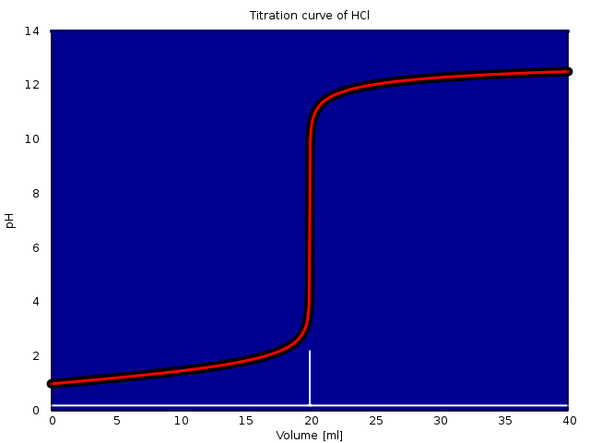
Das erste Beispiel ist HCl — der pH-Sprung ist maximal, der rein blaue Hintergrund zeigt an, daß freie HCl niemals vorkommt. Die Pufferwirkung (flache Kurve) kommt aus dem extremen pH-Wert von kleiner 2 bzw. größer 12 am Anfang und Ende der Titration, dazwischen liegt der Sprung.
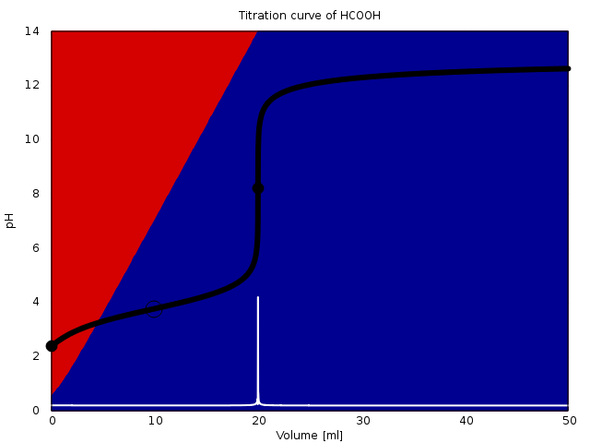
Das zweite Beispiel ist Ameisensäure mit dem pKₐ 3.77. Am Anfang liegt fast alles in Form von Ameisensäure vor, die wird am Weg zum Äquivalenzpunkt linear abgebaut, am Äquivalenzpunkt ist keine mehr da, und der pH springt.
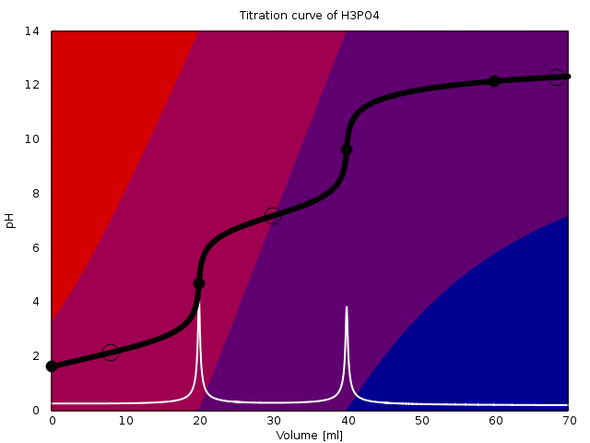
Das dritte Beispiel ist die Phosphorsäure mit drei Dissoziationsstufen, aber nur zwei pH-Sprüngen (pKₐ=2.148, 7.198, 12.319). Die ersten beiden Äquivalenzpunkte funktionieren ungefähr so wie bei der Ameisensäure, aber der letzte ist nicht zu sehen, weil das PO₄³⁻ zu stark hydrolysiert, d.h., es gibt keinen Moment, indem alles Phosphat als PO₄³⁻ vorliegt.
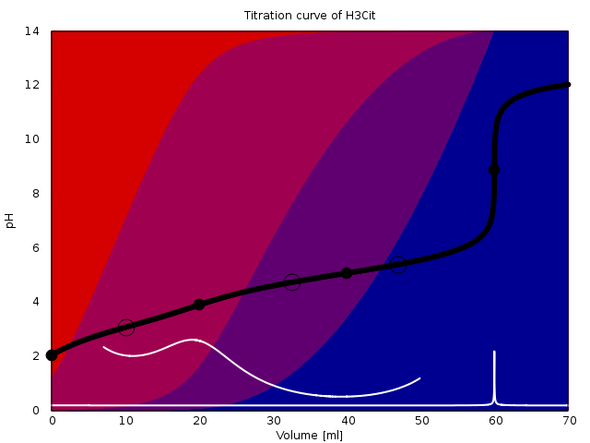
Noch schlimmer ist es beim vierten Beispiel, der Zitronensäure (pKₐ=3.09, 4.75, 5.41). Die drei pKₐ-Werte liegen so eng zusammen, daß an den ersten beiden Äquivalenzpunkten immer mehrere Spezies nebeneinander vorliegen, daher puffert die Lösung, daher kein pH-Sprung; statt−dessen sieht man nur am Ende, bei dritten ÄP, einen riesigen Sprung.
Das fünfte Beispiel zeigt Dir etwas, was Du wahrscheinlichnoch nie gesehen hast: Carnosin Hydrochlorid (pKₐ=2.73, 6.87, 9.73). Hier sind alle drei Äquivalenzpunkte passabel sichtbar, weil an den ÄP jeweils eine Spezies dominiert (beim zweiten und dritten ÄP ist es nicht ganz exakt, da findet man leichte Beimengungen anderer Spezies, deshalb sind auch die Sprünge nicht so schön).

Weil ich 20 ml einer 0.1 mol/l Lösung der Säuren mit 0.1 mol/l NaOH titriere.

1) Sprung: Du hast 100 Ententaler im Geldbeutel und gibst alle 10 Minuten 10 davon aus.
Das erste Mal schrumpft das Vermögen um 10%, das zweite Mal um gut 11% usw. Die Relation der verbliebenen H3O zum Lösungsmittel (bei Basenzusatz) gehorcht demselben Gesetz. Die logarithmische Skala dämpft diesen Effekt sogar (daher wurde sie eingeführt).
2) Titriert man eine schwache Säure mit einer starken Base, so verhält sich das Kapital H3O so, als würde nach jeder Ausgabe ein Teil wieder ersetzt. (passiert auch, die Säure dissoziiert nach) Dadurch ist der pH-Anstieg nicht so stark
Weil der pH-Wert eine logarithmische Skala ist.

Wieso ist jetzt der Äquivalenzpunkt bei 20ml?