Wie kann ich einfach/ online das Volumen eines Unregelmäßigen Körpers berechnen?
Hallo,
ich möchte das Volumen/ das Gewicht eines etwas komplizierteren Körpers berechnen.
Ich würde das Gern Online machen, da ich schnell änderungen durchführen möchte.
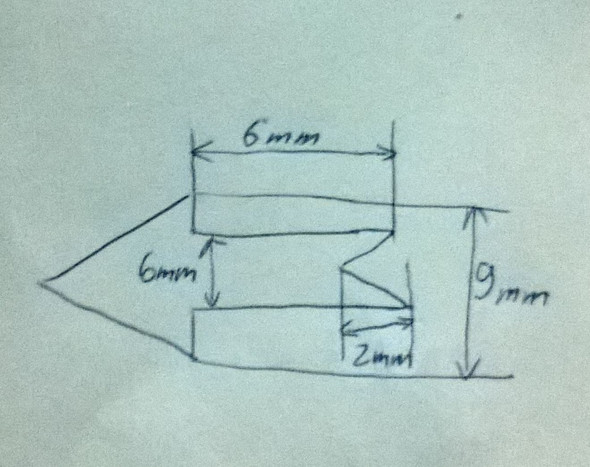
Das Foto zeigt eine Skizze des Körpers. Ich möchte hauptsächlich den Schwerpunkt des Körpers berechnen um genau zu wissen wie lang die Spitze sein müsste, damit der Schwerpunkt an einer Bestimmten Stelle liegt.
Danke schon mal an alle die nicht schreiben: "Schau bei Google", denn das habe ich bereits getan und nichts vernünftiges gefunden.
5 Antworten

Ich habe erstmal eine Maßstabs-Gerechte Zeichnung angefertigt.
Das ist ein Rotations-Körper, der sich aus Kegel- und Zylinder-Elementen zusammensetzt:
Die Pfeilspitze ist ein Kegel, bei dem die Höhen-Angabe fehlt
( beim Zeichnen hatte sich zufällig eine Höhe h von 6mm ergeben )
, mit 9 mm Kreis als Grundfläche.
Daran schließt sich ein Zylinder der Höhe 6mm mit 6mm Durchmesser an. Von diesem ist ein Kegel der Höhe 2 mm und dem Grundflächen-Kreis 6mm abzuziehen.
V[Kegel]=(1/3)*pi*(r^2)*h
V[Zylinder]=pi*(r^2)*h
V[Gesamt] = V[Spitzen-Kegel] + V[Zylinder] - V[Schweif-Kegel]
Kompliziertere Körper werden über Das Integral ihrer Rotationskurve berechnet. Eine Online-Anwendung hierfür ist mir nicht bekannt.
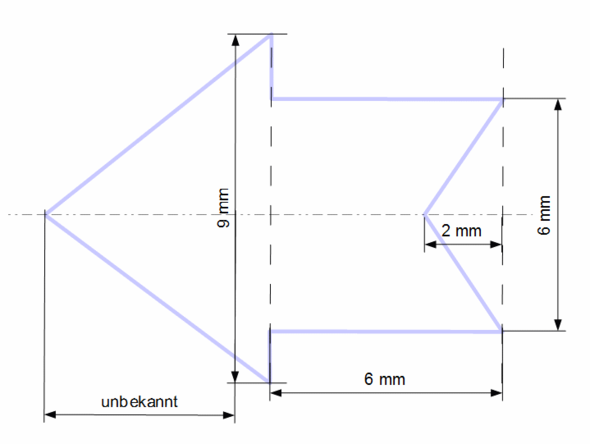

Kompliziert aufgebaute Körper kann man berechnen, indem man sie in beliebig viele einfacher zu berechnende Körper unterteilt, zum Beispiel in Quader, Pyramiden, Kegel, Zylinder und so weiter, und dann die Teilvolumina dieser einfacheren Körper addiert.
Wenn das Ergebnis nicht 100 % exakt sein muss, sondern ein bestimmter Fehlerbetrag erlaubt ist, dann wird es selbst bei den kompliziertesten Körpern entsprechend einfacher.
Da der Unregelmäßigkeit echter dreidimensionaler Körper im Prinzip keine Grenzen gesetzt sind, wirst du nicht einfach mal eben so ein Gratis - Programm im Internet finden, welches dir auf Knopfdruck alle Arbeit abnimmt.
Ich kenne kein derartiges Programm, aber wenn es so etwas gibt, dann kostet es bestimmt eine ganze Menge Geld, zumindest kann ich mir das vorstellen.

hi,Disturpedman!
du könntest den gegenstand in wasser tauchen.danach kannst du die dichte des materials online schnell nachschlagen,und am ende mit deinem volumen erweitern.

Der Körper existiert noch nicht. Desshalb möchte ich ihn berechnen, bevor ich das Teil auf der Drehbank baue.

Jetzt mal ganz per Hand, so kompliziert ist der Körper ja nicht - zumindest wenn man mal davon ausgeht, dass du das ganz im Prinzip rotationssymmetrisch aufbaust (bis auf die Kerbe am Ende)
Du hast einen Kegel als Spitze, der hat das Volumen
V_Spitze = 1/3 * Pi * 4,5² * l_Spitze
l_spitze ist die Länge der Spitze, 4,5 der Radius der Grundseite des Kegels.
Dann hast du einen Zylinder mit der Höhe 4 mm (= 6-2) und einem Durchmesser von 6 mm
V_Zylinder = 4 * 3² * Pi
Und schließlich kleben an dem Zylinder noch zwei Zylinderhufe mit halbkreisförmiger Grundfläche (das macht die Berechnung erstaunlich einfach) dran:
V_Hufe = 2 * 2/3 * 3² * 2
Ich nehme jetzt mal an, dass du einen Schwerpunkt suchst, der irgendwo innerhalb des Zylinderabschnitts liegen soll (alternativ könnte der Punkt auch innerhalb der Spitze liegen, wenn du das meinst, musst du anders rechnen). Wegen der Symmetrie des Objekts ist ja schon mal klar, dass der Punkt sich auf der Mittelachse des ganzen herumtreibt.
Links des Schwerpunkts liegt dasselbe Volumen wie rechts davon. Links davon findet man V_Spitze und einen Anteil von V_Zylinder, nämlich
V_Zylinder_links = x * 3² * Pi
Rechts davon findet man V_Hufe und den Rest von V_Zylinder, nämlich
V_Zylinder_rechts = (4-x) *3² * Pi.
Dabei bezeichnet x die Lage des Schwerpunkts, gerechnet von der Trennlinie zwischen Kegelspitze und Zylinder.
Das kann man jetzt alles in eine Gleichung packen:
V_Spitze + V_Zylinder_links = V_Hufe + V_Zylinder_rechts.
Dann bekommst du eine Gleichung, die du so umstellen kannst, dass am Ende l_Spitze abhängt von x.
Ist es das, was du suchst?

Integralrechnung online? Wäre mir neu. Aber kannst ja mal suchen....