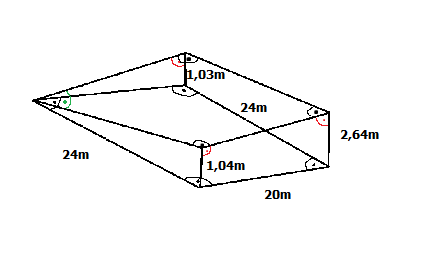
Hi. Kann jemand das Volumen dieses speziellen unregelmäßigen Körpers aus den vorhandenen Daten ermitteln? Keine Daten im Netz gefunden?
Es gibt weder einen Online-Rechner noch freeware-Programm. Auch eine sinnvolle Formel zum selbst berechnen habe ich nicht gefunden. Muss man da evtl. alles in einzelne Teile zerlegen und am Ende addieren?
4 Antworten
Liegen die 4 oberen Punkte in einer Ebene?
Wenn ja - dann:
V = 1/2 * 20m * 24m * 2.64m
= 633,6m³
Du kann das als Funktion z = f(x, y) auffassen.
Die Seite die 24 m lang ist, die nenne ich die x - Achse
Die Seite die 20 m lang ist, die nenne ich die y - Achse
Die Höhe nenne ich die z - Achse
Wertetabelle x | y | z
0 | 0 | 0
24 | 0 | 1.04
0 | 20 | 1.03
24 | 20 | 2.64
Für x = 0 -->
0 | 0
20 | 1.03
g = 0 + 0.0515 * y
Für x = 24 -->
0 | 1.04
20 | 2.64
g = 1.04 + 0.08 * y
Die Koeffizienten von g können nun als Funktion von x aufgefasst werden.
Erster Koeffizient -->
0 | 0
24 | 1.04
h = 0 + (13 / 300) * x
Zweiter Koeffizient -->
0 | 0.0515
24 | 0.08
h = 0.0515 + 0.0011875 * x
------------------------------------------------------------------------------------------------
z = f(x, y) = (13 / 300) * x + (0.0515 + 0.0011875 * x) * y
Diese Funktion beschreibt von
0 <= x <= 24
und
0 <= y <= 20
exakt (!!) die Höhe von der Funktion über Null, wenn man die untere Kante deines Objektes als auf der Nullebene liegend ansieht.
Leider weiß ich nicht, wie man den Rauminhalt von Funktionen der Form z = f(x, y) berechnet ;-((
Ich habe ernste Zweifel ob eine Berechnung auch mit einem tool gelingen kann, weil ein paar Maße fehlen. Gerade die obere Fläche ist durch vier Höhenpunkte gestützt, die noch nicht einmal in einer gemeinsamen schiefen Ebene liegen. Das bedeutet, dass die obere Fläche irgendwie gekrümmt ist.
Nun könnte es sein, dass die schwarz markierten Ecke Rechtecke sind. Aber selbst diese Annahme kann in Deinem Bild nicht überall widerspruchsfrei angewandt werden. Und was bedeuten die grünen und die roten Ecken; und manche Ecken sind gar nicht markiert. Gibt somit vier verschiedene Kriterien von Ecken?
Das einfachste wäre, wenn Du eine Tetraeder-Zerlegung des Körpers liefern könntest. Das erreichst Du schon, wenn Du Angaben zu einigen diagonalen Abmessungen liefern könntest. Dann könnte man genüsslich drauf los rechnen.
Ich denke ja, muss man irgendwie zerlegen. Vielleicht in eine Pyramide (linker Teil) und dann den Rest irgendwie.
...mit einem Zweifachen Integral. ;-)