Welchen Flächeninhalt hat das Rechteck im Quadrat? (Extremwertprobleme / 9. Klasse / Gymnasium?
Hallo Leute,
ich lerne gerade auf eine Mathe Schulaufgabe am Dienstag und bin bei einer Aufgabe am verzweifeln.
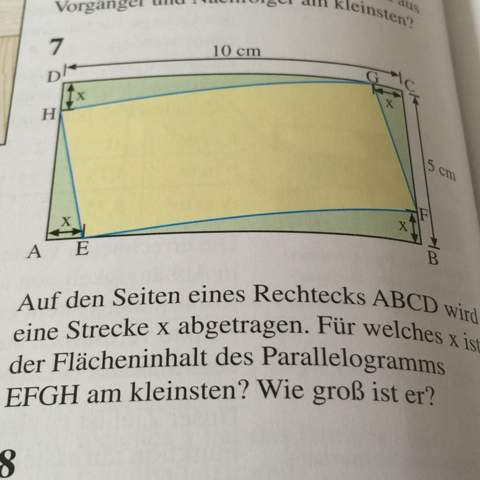
Ich habe sie abfotografiert. Bitte helft mir. Es geht um ein Extremwertproblem. Ich denke das Niveau ist auch nicht zu hoch.
Danke schon mal im Voraus.
Lg
3 Antworten

Fläche (parallelogr.) = Rechteck - 4 Dreiecke
A = 50 - [2 • 1/2 • x(10-x) + 2 • 1/2 • x(5-x)]
Klammer lösen; gleiches zusammenfassen;
A ' = 0

also um die Fläche des Parallelogramms auszurechnen..
10*5-(2* x*(10-x)/2 + 2* x*(x-5)/2 ) = 10*5 - (x*(10-x) + x*(5-x)) = 50+2x^2-15x. also f(x) =2x^2-15x+50 f'(x) = 4x-15 ... dann setzt du die erste Ableitung gleich 0 .. 0=4x-15 also 4x=15 und erhälst x = 15/4

Bei solchen "Flächenaufgaben" gilt immer A=große Fläche - kleine Fläche
Fläche des Parallelogramms Ap ist gesucht
große Fläche ist das Rechteck Ar
und wir sehen 4 rechtwinklige Dreiecke (2 gleiche Kleine A1 und 2 größere A2
es gilt somit Ap=Ar - 2 *A1 - 2 *A2
Fläche des rechtwinkligen Dreiecks ist A=1/2 * a *b
A1=1/2 * x(AD-x)=AD *1/2 * x - 1/2 *x^2
A2= 1/2 * x (AB-x)=AB*1/2 * x - 1/2*x^2 eingesetzt
Ap=Ar- AD * x +x^2 -AB *x + x^2 mit Ar=50 cm^2 AB=10 cm AD=5 cm
ergibt Ap=50 -5 *x +2 *x^2 -10 *x=2 *x^2 -15 *x +50
abgeleitet ergibt sich A´p(x)=4 * -15 Nullstelle bei x=3,75 cm eingesetzt in
Ap=21,875 cm^2
nochmal abgeleitet A´´p(x)=4 Größer Null
Bedingung für ein Minimum f´(x)=0 und f´´(x) >0