Stimmt die Aussage: Die Geraden sind nur zueinander parallel,wenn Winkelpaare zusammen 180 Grad ergeben.?

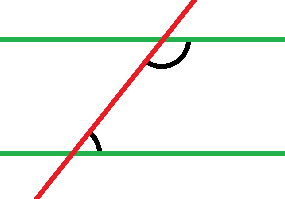
Wenn Du damit meinst, dass die beiden in meinem Bild schwarz eingezeichneten Winkel zusammen 180° ergeben, dann stimmt Deine Aussage.

Die Aussage gilt in beide Richtungen: Wenn Nachbarwinkel zusammen 180° ergeben, sind folglich die Geraden parallel. Und wenn die Geraden parallel sind, dann ist folglich die Summe der Nachbarwinkel 180°.

(s. https://de.wikipedia.org/wiki/Winkel#Nachbarwinkel_oder_E-Winkel)

Das lässt sich z. B. aus den Sätzen über Neben- und Stufenwinkel herleiten. 

Das hört sich etwas seltsam ab.
Gemeint ist wohl, dass Wechselwinkel an Parallelen gleich sind.
In der Umkehrung:
bei Vorhandensein von gleichen Wechselwinkeln sind die freien Schenkel parallel.

Nebeneinanderliegende Winkel an einem Punkt auf einer Geraden addieren sich zu 180°. Das ist natürlich auch wahr.

Wenn ich das Richtig verstehe, stimmt das, wenn die Winkel auf einer Geraden nebeneinander lieben.