Statisktik: p-wert berechnen mit formel ?
Hallo, möchte den p-wert anhand dieser formel berechnen. bekomme das aber mit meinem simplen taschenrechner nicht hin. kann vielleicht einer von euch p- mithilfe der formel (siehe bild) berechnen. n=129 t=8,67534 (falls gebraucht r=0,61) würde mich über antworten sehr freuen.
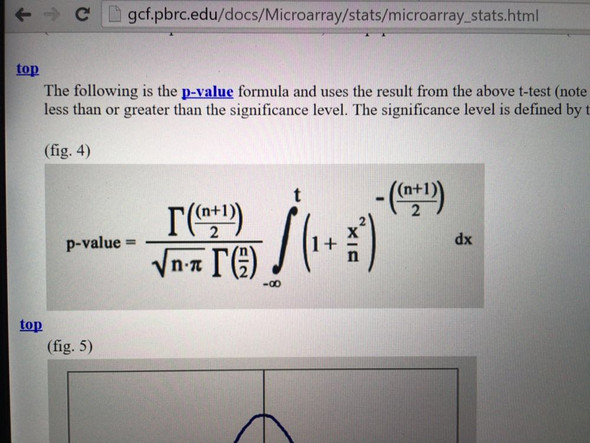
2 Antworten
Sag doch gleich, dass Du die CDF der Studentischen-t-Verteilung suchst :-)
http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
siehe Bild ( Dezimaltrennzeichen ist Punkt!)
Herleitung des Integrals per hypergeometrische Funktion:
integral (1+x^2/n)^(-n/2-1/2) dx
= x * 2F1(1/2, (n+1)/2, 3/2, -x^2/n)
= x-((n+1) x^3)/(6 n)+((n^2+4 n+3) x^5)/(40 n^2)-((n^3+9 n^2+23 n+15) x^7)/(336 n^3)+...
Das Vordere ist die Gammafunktion -> hat die Dein Taschenrechner?
Welches Modell hast Du? Bei einigen nennt sich das anders...
Wie viele Nachkommastellen brauchst Du?
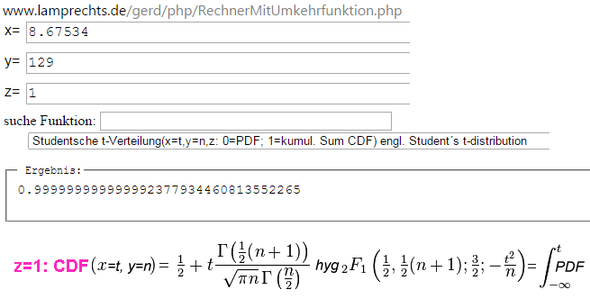
Welcher online-Rechner genau behauptet diesen völlig danebenliegenden Wert? (das ist weder PDF noch CDF)
Nur 5 Stellen genau?? Selbst das billigste Javascript kann 15 Stellen.
a) oft gibt es unterschiedliche Fragen zur Integrationsgrenze! Die Formel von Dir beginnt bei -unendlich = -∞
.
Wenn man von t bis unendlich rechnet (oder fragt), ist das genau der Rest, da das Volle Integral (100% Wahrscheinlichkeit von -∞ ... +∞ )
1-0,999999999999992377934460813552265
=0,00000000000000762206553918644774
b) wenn man PDF (Wahrscheinlichkeitsdichte; beim Umkehrfunktionen Rechner z=0) berechnet, kommt
0.000000000000042293405910805241734
heraus.
Wenn Du willst, bastle ich Dir eine Näherungsformel für Dein Rechner, aber dazu brauche ich die Anzahl der Nachkommastellen (gewünschte Genauigkeit)
c) Da von Dir r=0,61 kommt, kann es auch was völlig anderes sein, denn ein r gibt es in dieser Formel nicht!
Auch das n=129 scheint mir extrem hoch. So weit gehen kaum Tafelwerke...
Oder will ein Lehrer das Ergebnis "rund 1" hören?
http://www.socscistatistics.com/pvalues/pearsondistribution.aspx
mit diesem online rechner habe ich für p ein anderes Ergebnis herausbekommen
Danke für die Antwort. Dieser Rechner berechnet aus dem
Person-Korrelationskoeffizienten r
die 2-Seitige Restwahrscheinlichkeit (1-CDF(t,n-2))*2
der Studentischen t-Verteilung!
Das ist bei
http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
die Studentische t-Verteilung mit Sonderfall z=2
auf 33 Stellen mit allen Formeln!
Dein LINK-Rechner kann nur bis n=35 rechnen und nur 6 Stellen genau -> kleinere Werte als 0.00001 kann er nicht!
Kann man nicht berechnen, deswegen gibt es ja die Tabellen.
es handelt sich nämlich um einen korrelations koeffizenz untersuchung
zu "kann man nicht berechnen"
wir sind doch nicht mehr im Mittelalter/Renaissance...
Jedes Schulkind hat Handy mit Hochleistungs-CPU...
...und selbst wenn die Programmierfähigkeit nicht so gut ist (alles mit iPxxxx lässt ja nur das Laden von Apps zu statt den User selbst was programmieren zu lassen),
kann man sich bei
http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
die Ergebnisse berechnen lassen.
mein Taschenrechner ist ein Texas Instruments CAS. der hat das leider nicht. mich wundert nur dass solch ein hoher wert raus kommt für p. im online rechner für p kommt da 0,00001 oder so raus... was kann da schief gelaufen sein??