Skalarprodukt koordinateninvariant?
Guten Tag,
ich bin auf folgendes Beispiel in der Tensoralgebra gestoßen. Man beachte, dass die Indizes von den Koordinaten der Vektoren oben stehen.

Die letzte Zeile verstehe ich nicht. Das Skalarprodukt ist ja koordinateninvariant. Wieso hat es dann für die Vektoren bzgl. der Basis B den Wert –1 und nicht 0?
Oder bezieht sich die Koordinateninvarianz nur auf kartesische Koordinatensysteme?
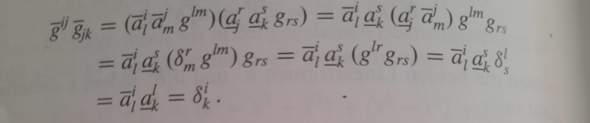
Werden hier nicht mehrfach Summen "auseinandergezogen" im Sinne der Einstein'schen Summationskonvention?
Denn weiter steht, dass man die Faktoren vertauschen darf, da es alle reelle Zahlen seien. Aber z.B. ist a_m^j * g^(lm) rechts des ersten Gleichheitszeichens doch eine Summe, muss also als ein Faktor betrachtet werden, oder nicht?
1 Antwort

Was genau du mit Koordinateninvarianz meinst, verstehe ich auf die Schnelle nicht - aber dass es einen Zusammenhang mit kartesischen Koordinatensystemen gibt, stimmt. Du kannst dir mit einer Scherung leicht klarmachen, dass der Zusammenhang zwischen "rechtwinklig im geometrischen Sinne" und "verschwindendes Skalarprodukt" in schiefwinkligen Koordinatensystemen nicht gilt.
Um hier herauszukommen, gibt es zwei Möglichkeiten:
Zum einen kann man erst ein Skalarprodukt einführen und danach die Winkel über das Skalarprodukt definieren (im Wesentlichen die vektorielle Formulierung des Cosinussatzes).
Zum Anderen kann man das Skalarprodukt für die "schiefe" Basis so definieren, dass es dieselben Werte annimmt wie für eine kartesische Basis. Dazu muss man natürlich beide Vektoren so transformieren, dass sie sich auf eine kartesische Basis beziehen; das entspricht je einer Matrizenmultiplikation. Wenn man die kartesische Basis entsprechend wählt, kommt man mit einer einzigen Matrix aus - man fasst Vektor a als Zeilenvektor auf und Vektor b als Spaltenvektor und bildet ein Produkt mit einer Matrix G dazwischen
(a, b) := a · G · b
wobei man G den "metrischen Tensor" der Basis nennt.
Was auf dasselbe hinauskommt wie diese zweite Möglichkeit, aber die Transformationen an eine andere Stelle verschiebt, ist die Einführung von "kovarianten Koordinaten":
Die "üblichen" (in der Schule verwendeten und auch sonst gebräuchlichen) Koordinaten nennt man "kontravariant", weil sie sich umgekehrt verhalten wie Basistransformationen. Wenn man die Länge der Basisvektoren verdoppelt, muss man die einzelnen Koordinaten eines Vektors halbieren, damit es derselbe Vektor bleibt. Wenn man die Basisvektoren mit einer Matrix transformiert, muss man die Koordinaten eines Vektors mit der inversen Matrix transformieren.
Es gibt auch "kovariante" Koordinaten, die etwas weniger anschaulich sind (jedenfalls solange man sich nicht daran gewöhnt hat) - siehe etwa http://walter.bislins.ch/physik/index.asp?page=Kovariante+und+Kontravariante+Komponenten#H_Vektorkomponenten_in_einem_schiefen_Koordinatensystem
Diese Koordinaten transformieren sich ebenso wie die Basisvektoren (der originalen schiefwinkligen Basis), verdoppeln sich also z. B., wenn man die Längen der Basisvektoren verdoppelt.
Üblicherweise stellt man kontra- und kovariante Komponenten so dar, dass man die Indizes von kontravarianten Koordinaten rechts oben und die Indizes von kovarianten Koordinaten rechts unten an das Vektorsymbol schreibt.
Man kann as aber auch über Spalten- und Zeilenvektoren ausdrücken: die üblichen kontravarianten Koordinaten werden als Spaltenvektor notiert, die kovarianten Koordinaten als Zeilenvektor. Dann steckt die eigentliche Arbeit in der Umwandlung von Spalten- in Zeilenvektoren und/oder umgekehrt (die "Transposition" ist also kein einfaches Abschreiben mehr). Dafür lässt sich das Skalarprodukt wie gewohnt ausrechnen - man fasst den Spaltenvektor als 1×n- und den Zeilenvektor als n×1-Matrix auf, das Skalarprodukt von a und b ist dann
( b^1 )
( )
a · b = ( a_1, a_2, a_3 ) · ( b^2 ) = a_1 b^1 + a_2 b^2 + a_3 b^3
( )
( b^3 )
Der Vorteil von kartesischen Koordinaten ist, dass kontra- und kovariante Komponenten dieselben Werte haben.

man fasst Vektor a als Zeilenvektor auf und Vektor b als Spaltenvektor und bildet ein Produkt mit einer Matrix G dazwischen
(a, b) := a · G · b
wobei man G den "metrischen Tensor" der Basis nennt.
Genau so ein Metriktensor folgte darunter auf der Seite. Ich glaube, ich habe es verstanden.
Ich habe auch nochmal dort nachgeschaut, wo ich das mit der Koordinateninvarianz gelesen habe: Es handelte von kartesischen Koordinatensystemen.
Du hast mit sehr weitergeholfen (auch mit dem Link)! Vielen Dank für diese ausführliche Antwort!

Es sind ja alles endliche Summen, da darf man alle Summenzeichen nach ganz links ziehen, ohne dass sich das Ergebnis ändert. Ist nichts Anderes als Ausmultiplizieren.
Beispiel:
(a_i b^i) (c_j d^j)
= (a_1 b^1 + a_2 b^2) (c_1 d^1 + c_2 d^2)
= a_1 b^1 c_1 d^1 + a_1 b^1 c_2 d^2 + a_2 b^2 c_1 d^1 + a_2 b^2 c_2 d^2
= a_i b^i c_j d^j
Umgekehrt darf man auch die Summenzeichen nach rechts ziehen, solange nur das Ausklammern möglich ist, d. h. die Faktoren, die an den ausgeklammerten Summanden hängen, überall insgesamt dieselben sind. Aber das ist innerhalb der Einstein-Konvention so gut wie immer der Fall.

Also kann man bei so einem Ausdruck wie oben alle Summenzeichen nach links ziehen, ok.
Aber es tauchen bei Vertauschung der Faktoren ja auch noch neue Summen auf, wie z.B. eine nach dem Index r (zweite Zeile rechts).
Sowas verwirrt mich dann wieder, weil das Summenzeichen ja nicht schon seit Anfang an dort steht - weißt du, was ich meine?

Ganz am Anfang gibt es nur die Summation über j.
Im zweiten Ausdruck kommen die Summationen über l, m, r und s hinzu. Wieso man das machen kann, dazu müsste man wissen, was die a und g mit Über-/Unterstreichung bedeuten. Liegt hier dein Problem?
Im Weiteren fällt nur eine Summation nach der anderen weg durch das Kronecker-Delta.

Wieso man das machen kann, dazu müsste man wissen, was die a und g mit Über-/Unterstreichung bedeuten.
Das sind Einträge von Matrizen. Die mit dem Buchstaben a sind welche von einer orthogonalen Matrix (mit Unterstrich die der Inverse/Transponierte). g sind Einträge von ko- und kontravariante Metriktensoren.
Liegt hier dein Problem?
Ich glaube ja...

Es sieht mir danach aus, dass hier der metrische Tensor g einmal in seiner kontravarianten und einmal in seiner kovarianten Form auf dieselbe Weise transformiert wird. Die Umformungen dienen dann dem Nachweis, dass die Überschiebung des transformierten Tensors mit sich selbst ebenso die Einheitsmatrix ergibt wie die Überschiebung des originalen Tensors mit sich selbst. Vermutlich wird dann noch darauf hingewiesen, dass das bedeutet, dass orthonormale Transformationen die Metrik erhalten.

Prinzipiell verstehe ich das auch so, nur die Rechnung konnte ich eben nicht nachvollziehen.
Jetzt habe ich aber verstanden, dass die Summationskonvention auch gilt, wenn zwischen den Komponenten acuh welche sind, die andere Indizes haben - hauptsache bei zwei Komponenten steht der selbe einmal oben, einmal unten, egal ob Faktoren dazwischen sind.
So macht das jetzt für mich auch Sinn. Ich dachte zuerst, dass bspw. bei a_j^i c_k^j b_l^j nicht nach dem Index j summiert wird, sondern nur wenn der Teil mit c nicht dazwischen steht (von der Definition her).
Hey,
ich habe meine Frage ergänzt. Es geht um das Vertauschen von Faktoren wobei ich meine, dass Summen "gebrochen" werden - das Verstauschen der Faktoren also falsch ist.
Kannst du mir erklären, wieso man diese Tensoren(?) vertauschen darf?
Man beachte die Einstein'sche Summationskonvention.