Oberflächenintegral einer Kugel berechnen?
Das Oberflächenintegral einer Kugel lautet ja
Wobei der Winkel zwischen Radius r und x-Ebene und
der Winkel zwischen Radius r und z-Ebene ist. Richtig?
Was mich nun verwundert: woher kommt das:
Meinen Erfahrungen nach, ist der Umfang eines Kreises gegeben durch
Würde es nicht Reichen beide Umfänge zu multiplizieren?
Das würde auch auf die obige Formel kommen… nur ohne das eine halt.
2 Antworten

Hi, ich bin erst 12. Klasse und weiß daher nicht ob meine Antwort richtig ist, aber ich mag Mathematik, hab mich ein bisschen informiert und vielleicht hilft dir ja mein Verständnis weiter... 😅
Also die Grundidee ist ja, im Integranden die kleine Fläche der Kugel auszurechnen, die sich durch dphi und dtheta bildet.
Genauso wie man beim normalen Integrieren beim Integranden die Fläche unter der Funktion mit der Länge dx berechnet, die bei einem unendlich kleinen dx zu einem Rechteck mit f(x)*dx wird. Daher Integral(f(x)*dx)...
Wie kommt man auf die Fläche? Wenn dtheta und dphi unendlich klein werden, wird dieser kleine Teil der Oberfläche zu einem Rechteck. Ich habe hier mal von mathstackexchange eine Grafik genommen, die eigentlich für die Volumenberechnung gedacht war aber egal:
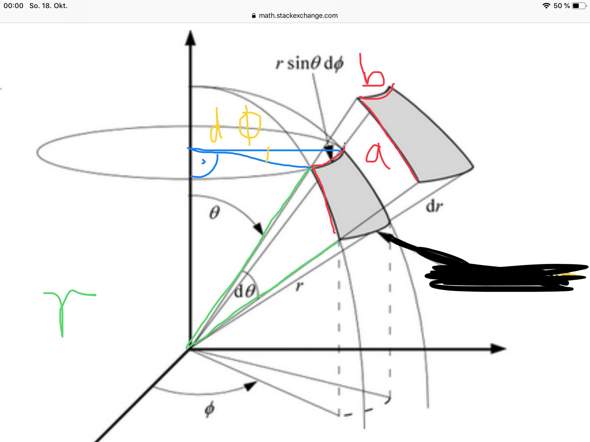
Wie gesagt, wenn dtheta und dphi unendlich klein werden, wird die Fläche zum Rechteck mit A=a*b, was dann im Integral steht.
Die blaue Seite lässt sich im Rechtwinkligen Dreieck berechnen mit r*sin(theta).
Für Kreissegmente oder wie auch immer man die nennt gilt:
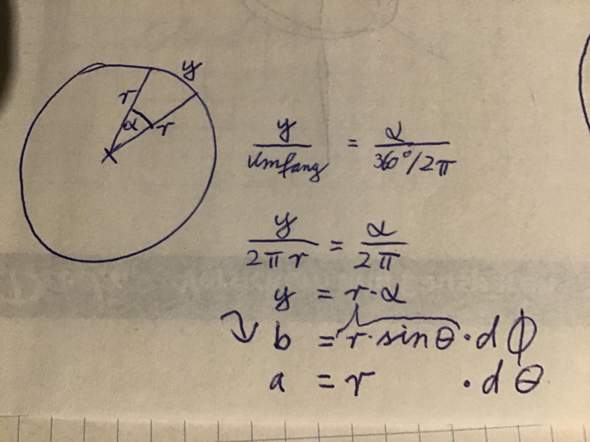
Also für die Seite b der Fläche ergibt sich mit der blauen Seite und dem Winkel dphi (gelb) : b=r*sin(theta)*dphi
und für Seite a mit der grünen Seite (Radius) und dem Winkel dtheta: a=r*dtheta
Für den Integranden ergibt sich also für die Fläche A bzw dA:
A bzw. dA= a*b = r*dtheta*r*sin(theta)*dphi = r^2 sin(theta)dtheta dphi
Wenn man nur r^2 hätte, ohne Sinus theta, dann würde die obere Seite des „Rechtecks“ gleich groß bleiben, egal wo dtheta und dphi liegen, bei der Kugel wird die Obere Seite bei den (unendlich kleinen) Rechtecken aber nach oben und unten hin in der Kugel kleiner, weshalb das zu einem falschen Ergebnis führt (müsste ja dann irgendwie sowas wie ein Zylinder werden aber auch nicht ganz).
Hier gut zu erkennen:

Also zusammengefasst muss man den Sinusterm reinbringen, weil man ja im Integranden die Fläche eines kleinen Teils der Kugel unter den Winkeln dtheta und dphi berechnet, die Fläche aber unterschiedlich groß ist, je nachdem „wie hoch“/wo theta liegt. Mit nur r^2 würde man das nicht berücksichtigen, aber durch den Sinusterm wird die obere Seite der Fläche und damit die Fläche dementsprechend an die „Lage von theta“ angepasst.
Vielleicht konnte ich dir ja weiterhelfen, aber ich will nochmal anmerken dass das auch alles falsch sein könnte!! :)
Mit unendlich klein meine ich natürlich den Grenzwert, denn beim Integrieren gehen die d... gegen null ;)
Schreib doch gerne einen Kommentar falls du beim Verständnis noch weitergekommen bist (z. B. beim Auswerten), würde mich auch interessieren!




Das sollte dich nicht deprimieren! Hab auch relativ lange dran gesessen aber das macht mir halt Spaß :]
Meinst du die Bezeichnungen a und b vertauschen? Kannst du natürlich, dass a die obere Seite vom „Rechteck“ ist die kleiner wird, und b die Seite links/rechts die gleich bleibt. Dann ist aber die Formel für a = r*sin(theta)*dphi, ohne dphi wäre es ja die blaue Seite.
An der Flächeninhaltsformel fürs Rechteck A=a*b ändert das ja nichts. :)
Hab ich deine Frage richtig verstanden? 😅

Ja, es ist alles ganz klar jetzt. Was mich nur verwirrt hatte, war das a = r'*\dphi und b=r*d\theta ist, wobei r'= r*sin(theta). Ich dachte es ist der gleiche Radius r gemeint, aber man muss ja natürlich eine Abhängigkeit reinbekommen. Vielen Dank für diese Klarstellung ☀︎

Das
bzw. eigentlich das
kommt von der sogenannten Funktionaldeterminante. Diese ist die Determinante der Jacobi Matrix von der Funktion, welche kartesische in Kugelkoordinaten Umwandelt. Diesen Term brauchst du als Faktor, damit das Integral eben den richtigen Wert für die Kugelkoordinaten ausgibt (da es ja eigentlich für das kartesische Koordinatensystem gedacht ist).
Das brauchst du also immer, wenn du Kugelkoordinaten verwendest, also auch bei der Volumenberechnung oder sonstige sphärische Angelegenheiten.
Das deprimiert mich nun schon, dass du das augenscheinlich so gut verstehst, nicht schlecht. Also kann man aber auch a und b vertauschen also a = r*sin(\theta)?