Extremwertaufgaben?
Kurze Frage zu folgender Aufgabe
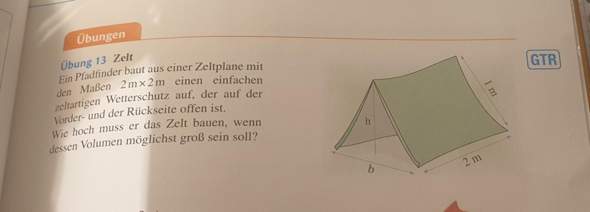
Die Hauptbedingung V=½h×b×2 ist klar. Die Nebenbedingung wird in den Lösungen mit 1=Wurzel(h²+b²/4) angegeben. Ich bin da aber irgendwie auf b²/2 gekommen. Weil ½b²+h²=1.
Wieso jetzt b²/4 ?
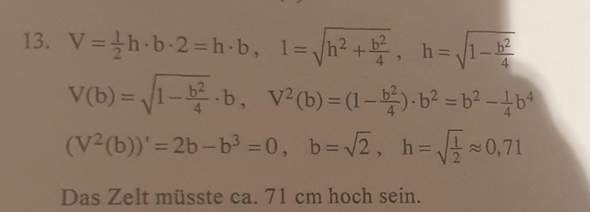
Hier die entsprechende Musterlösung
3 Antworten

Die Katheten sind b/2 und h, folglich gilt: (b/2)² + h² = (b²/4) + h² = 1²


Hallo,
die Sache wird viel einfacher, wenn Du b/2=x setzt.
Dann gilt nach dem Satz des Pythagoras x²+h²=1 (Nebenbedingung).
Die 2 m Länge sind für das Maximalvolumen unerheblich, da sie eine Konstante sind.
Das Volumen wird dann maximal, wenn der Zeltquerschnitt maximal wird, das wäre dann einfach h*x (x=b/2 ist die halbe Grundseite, h ist die Höhe des gleichschenkligen Dreiecks, das den Querschnitt bildet).
Du mußt also nur ermitteln, wann das Produkt h*x maximal wird, wenn die Nebenbedingung lautet, daß x²+h²=1.
h²=1-x² und h=Wurzel (1-x²)
Querschnittsfläche also x*(Wurzel (1-x²).
Ableiten nach x und Ableitung gleich Null setzen.
Ich selbst habe es mit dem Lagrange-Multiplikator gelöst und mit partiellen Ableitungen nach h, x und lambda, das ist einfacher.
Lösung auf jeden Fall x=h=Wurzel (1/2). Maßeinheit ist Meter.
Maximaler Querschnitt ergibt maximales Volumen.
Herzliche Grüße,
Willy

Kleiner Tipp, wenn h*x maximal, dann auch h²*x².
Wenn Du damit als Zielfunktion arbeitest, löst sich die Sache viel einfacher auf.

Hinweis: V=1/2*h*b*2 ist schon mal falsch,weil das die Fläche von 2 rechtwinkligen Dreiecken ist und damit die Frontfläche und kein Volumen.
außerdem muß da stehen A=1/2*h*(b/2)*2 → A=1/2*h*(b/2) ist ein rechtwinkliges Dreieck
Fläche von rechtwinkligen Dreieck A=1/2*a*b
Das kann man viel einfacher rechnen.
Damit das Volumen maximal wird,muß ja die Vorderfläche maximal werden,weil ja die Länge des Zeltes l=2 m=konstant ist
Das gleichschenklige Dreieck (Vorderfläche),kann in 2 rechtwinklige Dreiecke aufteilen.Die Vorderfläche wird dann maximal,wenn die Fläche des rechtwinkligen Dreiecks maximal ist
Fläche vom rechtwinkligen Dreieck A=1/2*a*b Amax=1/4*c² bei Winkel (a)=45°
mit sin(a)=Gk/Hy=h/c → h=sin(45°)*1 m=0,707...=|1/2*Wurzel(2)| Betrag !
Herleitung
1) A=1/2*a*b Fläche vom rechtwinkligen Dreieck
2) sin(a)=Gk/Hy=b/c → b=sin(a)*c
3) cos(a)=Ak/Hy=a/c → a=cos(a)*c
2) und 3) in 1)
A=1/2*cos(a)*c*sin(a)*c=c²/2*cos(a)*sin(a)
siehe Mathe-Formelbuch,was du privat in jedem Buchladen bekommst
Kapitel,trigonometrische Funktionen,Produkte von trigonometrischen Termen
sin(a)*cos(b)=1/2*[sin(a-b)+sin(a+b)] mit (a)=(b)
...=1/2*[sin(0)+sin(2*a)
sin(a)*cos(a)=1/2*sin(2*a)
eingesetzt
A=c²/2*1/2*sin(2*a)=1/4*c²*sin(2*a) Maximum,wenn sin(2*a)=1 → (a)=45°
Probe: sind(2*45°)=sin(90°)=1
maximale Fläche der rechtwinkligen Dreiecks bei Amax=1/4*c²
bei Alpha (a)=45° und Beta (b)=45°
Bei dir
1) A=1/2*h*(b/2)*2=1/2*h*b Vorderfläche
2) c²=(b/2)²+h² Satz des Pythagoras c²=a²+b²
aus 2) h=Betrag Wurzel(c²-b²/4) mit c=1 m
in 1)
A(b)=1/2*Wurzel(1-b²/4)*b ableiten mit der Produktformel (u*v)´=u´*v+u´*v´
Konstantenregel (a*f(x))´=a*f´(x)
A(b)=1/2*(1-b²/4)^(1/2)*b
A´(b)=0=..... Nullstellen ermitteln b=...
A´´(b)=.... prüfen,ob Maximum oder Minimum
den Rest schaffst du selber