Auf wie viele Arten lässt sich der 2m lange Zollstock zu einem Dreieck knicken?
Momentan stehe ich vor einer Aufgabe, die ich nicht wirklich lösen kann. Ich habe bereits dazu eigene Überlegungen gehabt (siehe unten), aber komme dennoch nicht auf eine entsprechende Lösung. In der Aufgabe wird die Frage gestellt, auf wie viele Arten der 2m lange Zollstock (abgebildet im Buch, Bild hier angefügt) zu einem Dreieck geknickt werden kann. Mir ist die Dreiecksungleichung bekannt und an dieser orientierte ich mich auch hauptsächlich.
Nun zu meinen Überlegungen:
Der Zollstock ist 2m lang, und hat 20 Knickstellen, von denen also eine Knickstelle genau 10cm lang sein muss. Ich habe orientierend an der Dreiecksungleichung festgestellt, dass die Schranke der beiden Seiten immer so zwischen 0,5m und 1m liegen muss. Ebenso darf die Summe der beiden Seiten natürlich auch nicht größer sein als der Umfang des Dreiecks, sondern eben nur größer als die dritte Seite (hier c).
Ich habe mir erst überlegt alle Kombinationen durchzugehen, und dabei Aufgaben an der Grenze notiert wie:
0,6m + 1,3m > 0,9m
0,7m + 1,2m > 0,9m
0,8m + 1,1m > 0,9m
0,9m + 1,0m > 0,9m
Zähle ich dann jeweils durch für den zweiten Summanden bis zur Grenze, komme ich beim ersten auf 9 Möglichkeiten, beim zweiten bei 8, beim dritten auf 7 Möglichkeiten und beim vierten auf 6 Möglichkeiten. Addiere ich die zusammen komme ich also auf 30 Arten wie man den Zollstock zu einem Dreieck knicken kann. Allerdings scheint das auch nicht zu stimmen, da ich hier noch andere Möglichkeiten übersehen habe.
Hier das Bild zur Aufgabe:
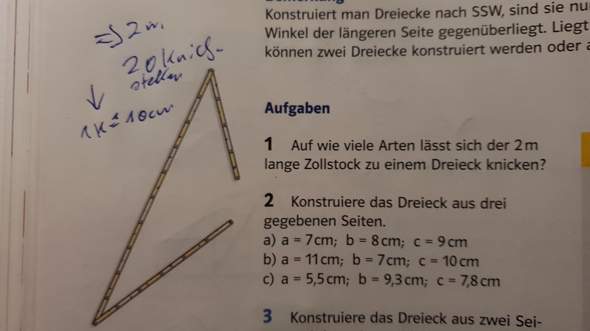
1 Antwort

Ein gewöhnlicher Zollstock kann an 9 Stellen im Abstand von 20 cm geknickt werden. Aber vielleicht hat der in der Aufgabe 19 Gelenke im Abstand von 10 cm.
Die längste Seite liegt zwischen 70 und 90 cm, denn bei 60 cm ist der Umfang höchstens 180 cm und bei 100 cm wird das Dreieck flach.
Die mittlere und kurze Seite findet man schnell durch Ausprobieren:
- 70 cm – verbleiben 130 cm = 70+60 cm
- 80 cm – verbleiben 120 cm = 80+40 = 70+50 = 60+60 cm
- 90 cm – verbleiben 110 cm = 90+20 = 80+30 = 70+40 = 60+50 cm
Zusammenzählen darfst Du jetzt selbst.
P.S.: Bei einem gewöhnlichen Zollstock sind davon nur zwei Lösungen möglich.

Also ich weiß, dass im Bild oben bei dem Zollstock 19 Gelenke sind. Allerdings verstehe ich nicht so genau in welchem Zusammenhang das mit der Aufgabe steht
Vergiss es einfach! Wenn man ein Intervall in n Teile teilt, hat man
- n–1 Schnittstellen
- n Teilstücke
- n+1 Randpunkte
Es ist ein beliebter Fehler, das durcheinander zu bringen. Deine „20 Knickstellen“ haben bei mir einfach einen Reflex ausgelöst. Für die Aufgabe ist das nicht relevant.

Handelt es sich hier übrigens um ein (triviales) Optimierungsproblem? Denn wenn ich das jetzt richtig verstehe, gibt es im Wesentlichen zwei Kriterien:
- Die Summe beider Seiten a und b müssen größer sein als die längste Seite c.
- Der Umfang muss 200cm betragen.
Also bedeutet das, dass sowohl a + b > c als aus a + b + c = 200cm (u = 200cm) gelten muss.

Handelt es sich hier übrigens um ein (triviales) Optimierungsproblem?
Fast. Zum Optimieren fehlt noch eine Zielfunktion. Aber sonst hat es alles, was ein MILP (Mixed Integer Linear Program) braucht: Ein Satz Variablen und lineare Ungleichungen.
Bei komplexen Optimierungsproblemen verwendet man den Simplex-Algorithmus. Wenn nur ganzzahlige Lösungen erlaubt sind, hängt man noch einen Branch-and-Bound hinten dran. Für alle ganzzahligen Lösungen gibt es kein brauchbares Verfahren, weil das in der Regel viel zu viele sind.
Hier sind es aber nur 3 Variablen und eine Gleichung, mit der man eine Variable komplett ersetzen kann (z.b. a := 200–b–c). So verbleibt ein Ungleichungssystem mit 2 Variablen:
- 200–b–c≥0 (statt a≥0)
- b≥200–b–c (statt b≥a)
- c≥b
- 200–c≥c (statt a+b≥c)
Solche kleinen Probleme löst man am Besten grafisch: Jede lineare Ungleichung entspricht einer Geraden, die die Ebene in einen gültigen und einen verbotenen Teil zerlegt. Zusammen umreißen sie ein Polygon, das alle gültigen Lösungen enthält. Hier ist es ein Dreieck.
Man muss kein Mathegenie sein, um alle ganzzahligen Gitterpunkte (genauer: alle Vielfachen von 10 bzw. 20) in diesem Dreieck abzuzählen. Mit etwas räumlichem Vorstellungsvermögen schafft man das auch bei Problemen mit 3 Variablen, aber darüber ist Schluss.
Die einzig mögliche Alternative wäre, das Problem in ein kombinatorisches Problem umzuformen (etwas in der Art „3 Nummern ziehen mit/ohne Zurücklegen“). Aber da sehe ich leider keinen brauchbaren Ansatz.

Vielen Dank für deine Antwort(en). Und dem Titel eines Experten absolut würdig ^^ Ich habe es jetzt verstanden und interessanterweise war die Aufgabe auch schwerer (auch wenn sie doch trivial ist) als die im Buch blau markierten Aufgaben (die eigentlich schwerer sein sollen). Und ja, falls man sich wundert, ich bin lediglich autodidaktisch unterwegs was die Mathematik angeht, also hab ich da keinen Lehrer, der mir bei sowas aushelfen kann :P Hoffentlich kann man mir das verzeihen

Und glaube auch zwei weitere Kriterien, nämlich das natürlich
a <= c
b <= c
sein muss.

Besser sogar noch a≤b≤c. Das ist zwar kein Muss, aber es reduziert die Zahl der Lösungen gewaltig.
Ich bin mir nicht sicher, was die Aufgabe unter „wie viele Arten“ versteht. Wenn es nur um die Kongruenz der Dreiecke geht, bist Du mit den abgezählten sortieren Werten fertig. Wenn die Reihenfolge der Seiten auf dem Stab einen Unterschied macht, musst Du für jede (sortierte) Lösung die Permutationen bilden. Das ist aber immer noch wesentlich einfacher, als alle Punkte ohne die Bedingung a≤b≤c zu bestimmen.
Erstmal vielen Dank für die Antwort. Nur leider verstehe ich gerade nur Bahnhof. Auch bei Hinzunahme eines echten Zollstocks mit 2m Länge, verstehe ich es leider immer noch nicht worauf du hier hinaus möchtest. (zugegeben mein Zollstock hat auch nur 9 Gelenke, wie es bei den meisten üblich ist) Durch Probieren konnte ich zumindest da etwas verstehen: Wenn ich das richtig verstanden habe, müssten also beim gewöhnlichen Zollstock folgende Lösungen möglich sein: 80+80+40 und 60+60+80. Aber kann man das irgendwie auch rechnerisch ermitteln? Also nicht unbedingt durch Probieren, sondern systematisch?
Okay, jetzt bei der eigentlichen Aufgabe zunächst ist mir unklar was du genau mit 19 Gelenken meintest. Also ich weiß, dass im Bild oben bei dem Zollstock 19 Gelenke sind. Allerdings verstehe ich nicht so genau in welchem Zusammenhang das mit der Aufgabe steht bzw. wieso ich gerade diese Zahl brauche. Ließe sich dazu etwa ein systematischeres Vorgehen finden, um die Aufgabe zu lösen statt probieren? Auch würde man doch mit "19" das letzte Stück Stock, das am Ende hängt, doch gar nicht berücksichtigen, oder? Kann man nicht genauso gut auch mit der Anzahl der Stöcke, die da dranhängen, arbeiten? (= 20)
Und die Zahlen bzgl. mittlerer und kurzer Seite kann ich auch nicht wirklich ganz nachvollziehen. Was genau sind hier die 70cm, 80cm, 90cm? Also sind das die Längen der längsten Seite? Also ich bin da etwas verwirrt. Entschuldige, wenn ich da nicht so ganz mitkomme.