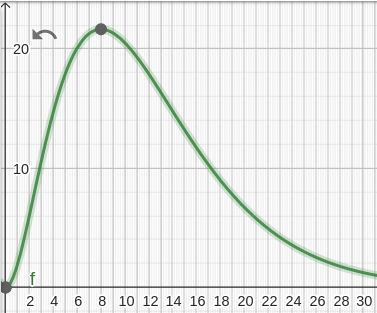
Was verwirrt denn da? Wie immer in der Kurvendiskussion ist da irgendeine Funktion gegeben (deren wahre Bedeutung völlig unwichtig ist und ob die irgendwas realistisch beschreibt ist auch - fast - ohne jeden Belang). Das einzig Unbekannte könnte sein, dass hier mal nicht "x" die Variable ist, sondern "t". Aber mehr ist da dann auch nicht.

Die Funktion gibt eine Konzentration an und Du sollst das Maximum der Konzentration suchen (Die Funktion gibt also schon einen Wert für eine Größe, deren Maximum Du suchen sollst).

Also wie immer Schema K(urvendiskussion):

• Erste Ableitung bilden (Nach "t" ableiten)
• Nullstellen der ersten Ableitung finden
• Zweite Ableitung bilden
• Nachprüfen welche Nullstelle(n) der ersten Ableitung eingesetzt in die zweite Ableitung kleiner Null ist/sind. Das ist/sind das/die Maximum/lokalen Maxima.
• Nun f(t) für den t-Wert des Maximums und schon hast Du die maximale Konzentration.

Nachtrag nach Kommentar:

Für die erste Ableitung erhalte ich (Deine Lösung aus dem Kommentar ist korrekt, ich habe hier nur zusätzlich noch die Exponentialfunktion ausgeklammert):



Davon Die Nullstellen mit dem Satz vom Nullprodukt:



Die zweite Ableitung ist (wieder die Exponentialfunktion ausgeklammert und die Terme zusammengefasst):

Nullstellen der ersten Ableitung einsetzen: