Extremaufgaben Mathe?
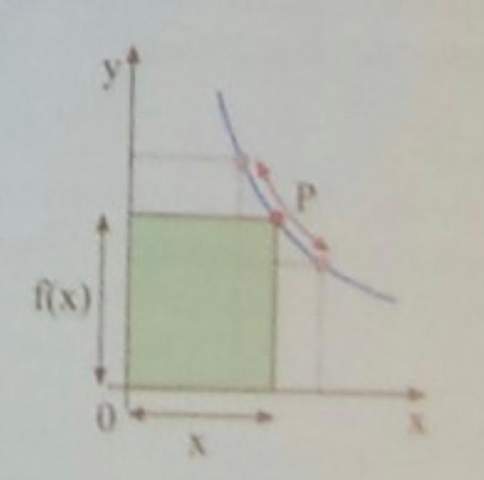
Zwischen Ursprung und Graph der Funktion f(x)=1+4/x^2 ist ein achsenparalleles Rechteck eingesperrt. Eine Ecke des Rechtecks ist der Ursprung, die gegenüberliegende Ecke P liegt auf dem Graphen von f.
Wie müssen die Koordinaten von P gewählt werden, damit der Flächeninhalt des Rechtecks minimal wird?
Das ist die Aufgabe und meine Frage ist, was hier die Nebenbedingung wäre und wie man dadrauf kommt? Den Rest habe ich.
Extremwertaufgaben,
Flächeninhalt
