Äquivalenzrelation - Theoretische Informatik?
Hallo Leute,
ich habe eine Frage zur Äquivalenzrelation. An sich habe ich die Relationen untereinander zu verstanden (reflexiv, symmetrisch und transitiv). Hier ist mal ein Beispiel. Die Äquivalenzrelation gilt für dieses Beispiel laut dem Prof.
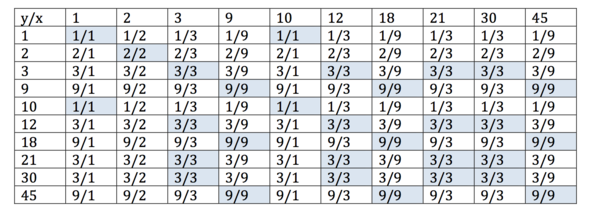
Gegeben ist die Menge M = {1, 2, 3, 9, 10, 12, 18, 21, 30, 45}. Jetzt soll man nachweise das die Relation R = {(x, y) ∈ M × M | x hat die gleiche Quersumme wie y} eine Äquivalenzrelation darstellt.
Das ganze wurde in einer Tabelle dargestellt (Tabelle im Anhang). Die Reflexivität und die Symmetrie zu beweisen ist kein Problem, aber wie stellt man hier die Transitivität da? Man hat ja nur x und y. Um die Transitivität darzustellen braucht man ja eigentlich auch jetzt z. Die Transitivität wird ja erfüllt wenn: Für x,y,z sind Elemente aus M. Wenn x R y und y R z dann folgt daraus das x R z ist. Aber woher bekomme ich das z jetzt?
Der Prof schreibt z.B. folgendes: Transitiv: Ja, denn wenn x1 und y sowie x2 und y die gleiche Quersumme haben, dann hat auch x1 und x2 die gleiche Quersumme. --> Wie ist das jetzt zu erklären?