Wie beweise ich Abgeschlossenheit von Mengen?
Hey, es wäre nett wenn mir jemand dabei helfen kann zu zeigen, ob eine Menge abgeschlossen ist oder nicht.
Wir haben Abgeschlossenheit wie folgt definiert:
Eine Teilmenge A von R bzw C heißt abgeschlossen, wenn der Grenzwert jeder konvergenten Folge von Punkten a_n∈A ebenfalls in A liegt oder A=∅ gilt.
- Also wenn etwas nicht abgeschlossen ist reicht es einfach eine konvergente Teilfolge zu suchen, die gegen einen Wert außerhalb von A konvergiert, oder?
- Wir haben jetzt folgende Menge gegeben:
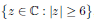
meine Vermutung ist, dass diese Menge nicht abgeschlossen ist, aber wie zeige ich das genau?
Annehmen, dass es eine konvergente Teilfolge a_n gibt, mit 6>=|a_n| f.a. n∈N und die gegen a konvergiert mit a∈{z∈C:|z|<6}. Wie führe ich das dann zum Widerspruch?
ich vermute, dass die Menge abgeschlossen ist*
4 Antworten

Wozu denn eine Teilfolge wählen, wenn die Folge nach Voraussetzung konvergent sein soll?

Annehmen, dass es eine konvergente Teilfolge a_n gibt, mit 6>=|a_n| f.a. n∈N und die gegen a konvergiert mit a∈{z∈C:|z|<6}. Wie führe ich das dann zum Widerspruch?
So einfach ist das nicht. Du mußt schon ZEIGEN, dass die gegen ein z mit |z| < 6 konvergiert, d.h. du mußt eine solche Folge explizit angeben oder wenigstens zeigen dass sie existiert. Ich vermute aber du wirst nichts finden. Meine Erfahrung ist dass >= oder <= ein starker Hinweis für Abgeschlossenheit ist.

Du kannst entweder das mit dem Komplement machen, wie ich geschrieben habe, oder zeigen, dass es Bälle gibt, wo z ein Element aus der Menge ist, aber der ε-Ball um z nicht vollständig in der Menge liegt

Nun, nimm eine Folge z_n mit |z_n| >= 6, die gegen z konvergiert und nimm an |z| < 6. Dann gibt es auch ein epsilon > 0, so dass |z + epsilon| < 6. Nun versuche mal |z-n - z| < epsilon zu bekommen.

Das ist genau die Stelle an der ich nicht weiterkomme.
Es gilt doch für beliebig viele z_n, dass |z_n-z|>epsilon ist und deshalb kann es so eine Folge nicht geben, also muss die menge abgeschlossen sein.

Genau. Daher ist die Voraussetzung |z| < 6 nicht haltbar. |z| ist damit >= 6, daher liegt z auch in der Menge und damit ist die Menge abgeschlossen.

und die Begründung ist so ausreichend? Ich fühle mich da immer so unsicher und traue mich dann nicht das aufzuschreiben...

Ich bin kein Tutor und meine Studienzeit liegt 30 Jahre zurück. Aber ich würde sagen ja.

Die Kurzfassung:
Nimm dir eine konvergente Folge (z_n) mit |z_n| >= 6, die gegen irgendein z konvergiert. Falls |z| >= 6 ist, gibt es nicht zu zeigen.
Ansonsten definiere a := 6 - |z| > 0. Per Voraussetzung gilt für hinreichend große Indizes n die Ungleichung |z - z_n| < a. Aber es gilt stets:
|z - z_n| >= ||z| - |z_n||
= |z_n| - |z|
>= 6 - |z|
= a,
im Widerspruch zu |z - z_n| < a.

Vielleicht hattet ihr so einen Satz wie: Eine Menge M ist abgeschlossen in X, wenn das Komplement von M, also X/M, offen ist

äh, hab mich verschrieben. Ich vermute, dass die Menge abgeschlossen ist. Deshalb wollte ich annehmen, dass sie nicht abgeschlossen ist, also so eine Teilfolge wie oben beschrieben existiert. Und dann würde ich halt versuchen auf einen Widerspruch zu kommen, also das so eine Teilfolge nicht existiert.
Edit: wie genau zeigt man das?